Решение простых линейных уравнений

Движение навстречу друг другу

Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:  

Задача 1Решение:Решение в виде выражения: 50 * (100 : 25) = 200Ответ
Задача 2

Решение:

1) 25 + 20 = 45 (сумма скоростей теплоходов)

2) 90 : 45 = 2

Решение в виде выражения:90 : (20 + 25) = 2

Ответ: Теплоходы встретятся через 2 часа.

Задача 3

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Решение:Ответ: Задача 4Решение:Ответ: Задача 5Решение:

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: Поезда встретятся через 4 часа.

Задачи на нахождение числа по доле и доли по числу

1. Руда на 4/5 состоит из меди. Сколько меди можно получить из одной тонны руды?2. 15 см — это 2/3 доски. Чему равна длина всей доски?3. При помоле на ржаную муку отходит в отруби 2/5 веса зерна. Сколько отрубей и сколько ржаной муки получится при помоле двух тонн зерна?4. Какой длины потребуется доска для прямоугольной рамки, если длина рамки 28 см, а ширина 4/7 длины?5. Длина дома 12 м, а ширина составляет 4/6 длины. Чему равен периметр дома?6. От мотка проволоки отрезали 2/5. Это 12 м. Чему равна длина всей проволоки?7. Сколько дней составляет 5/6 апреля?8. 4/5 кружки сахарного песка весят 200 г. Сколько весит кружка сахарного песка? 9. книге 68 страниц. Мальчик прочитал 3/4 книги. Сколько страниц осталось прочитать мальчику?10. В спортивной секции занимается 24 мальчика и несколько девочек. Число девочек составляет 3/8 числа мальчиков. Сколько всего человек занимается в спортивной секции?

Сложносочиненное предложение

Полные и худые подростки и решение проблемы гормонального сбоя Сложносочиненным (ССП) называют сложное предложение, имеющее два и более независимых простых предложений в составе. Это значит, что их можно разбить точкой, при этом смысл не потеряется.

Части таких сложных предложений связаны союзами и союзными словами: соединительными (и, да, также и т. д.), противительными (а, но, зато и т. д.), разделительными (либо, то… то, не то… не то и т. д.) или их комбинациями.

Примеры:

• Хотелось пирога, и яблоки уже созрели.

• Хотелось пирога, но яблоки еще не созрели.

• То мать пирогов напечет, то бабушка с булочками приедет.

Иногда части сложносочиненных предложений связаны без сочинительного союза и союзного слова — по смыслу. Такие предложения называют бессоюзными.

Пример:

Лето заканчивалось лихо: на улице резко похолодало, листья начали алеть и чахнуть.

Знаки препинания в сложносочиненных предложениях

В предложениях с союзами и, да, однако, либо и т.д. принято ставить запятую. Кроме случаев, когда:

Исключение
Если у частей сложного предложения есть общий второстепенный член или придаточное, но их соединяет повторяющийся союз, нужно ставить запятую.

Пример:

На ярмарке в городе показывали кукольные представления, и торговцы продавали сахарную вату, и зазывалы кричали приглашения на аттракционы.

В бессоюзных сложносочиненных предложениях части делятся не только запятыми, но и тире, двоеточиями и точкой с запятой. Эту тему мы подробно разобрали в статье о сложносочиненных предложениях.

Потренируемся

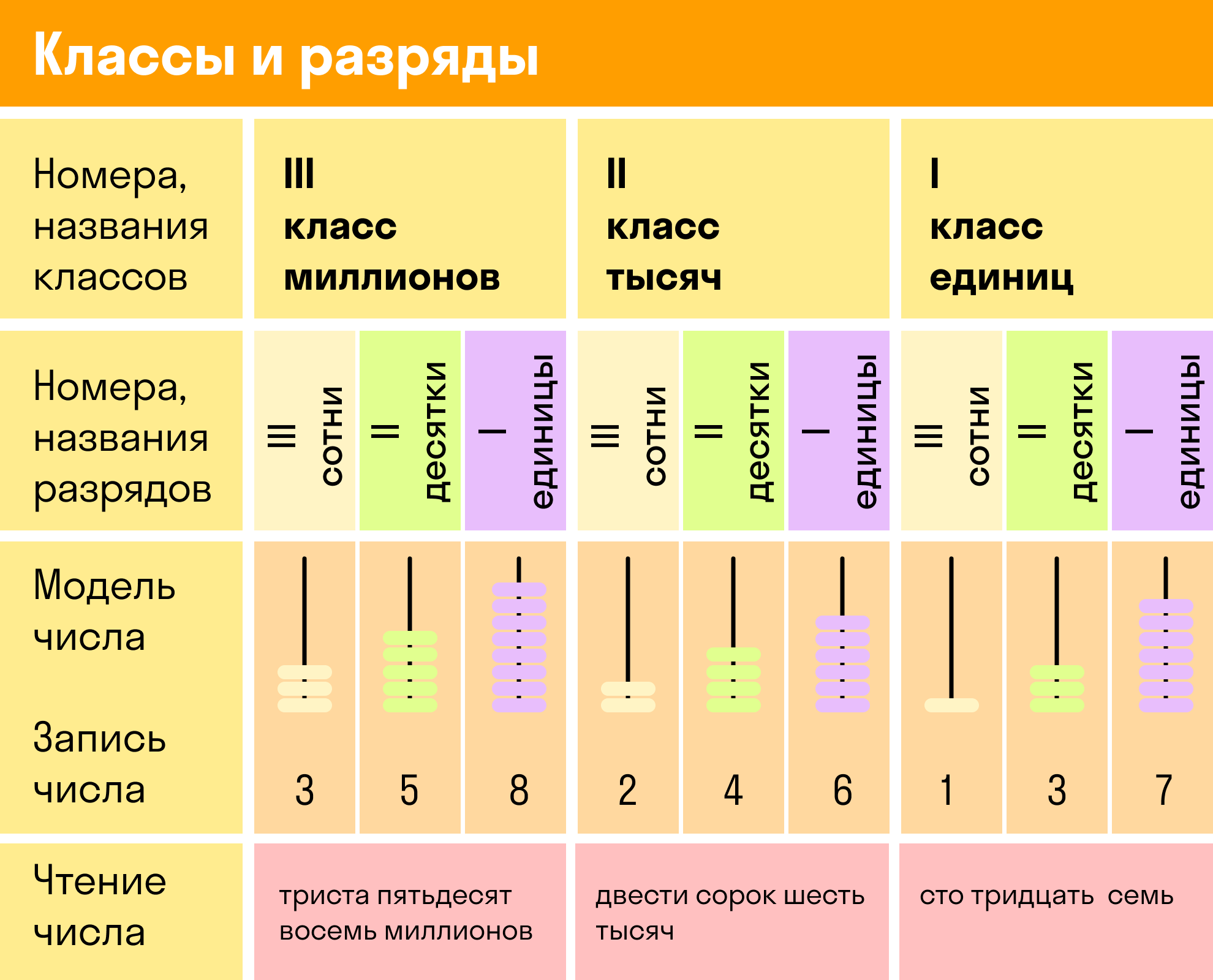
Пример 1. Записать цифрами число, в котором содержится:

1. 55 единиц второго класса и 100 единиц первого класса;
2. 110 единиц второго класса и 5 единиц первого класса;
3. 7 единиц второго класса и 13 единиц первого класса.

Ответ:

1. 55 100;
2. 110 005;
3. 7 013.

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

• 10 единиц равны 1 десятку;
• 10 десятков равны 1 сотне;
• 10 сотен равны 1 тысяче;
• 10 тысяч равны 1 десятку тысяч;
• 10 десятков тысяч равны 1 сотне тысяч;
• 10 сотен тысяч равны 1 миллиону.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

Как рассуждаем:

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

• 11 627 — одиннадцать тысяч шестьсот двадцать семь.
• 31 502 — тридцать одна тысяча пятьсот два.

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Сложноподчиненное предложение

Сложноподчиненное предложение (СПП) — это вид сложного предложения, в составе которого одно простое предложение по смыслу и интонации подчиняется другому. В этом случае зависимое предложение называется придаточным, а независимое — главным.

Пример сложноподчиненного предложения:

Мне было сложно понять, как ей удалось так быстро привыкнуть к новому городу.

Виды связи в сложноподчиненном предложении

Обычно части СПП в русском языке связаны друг с другом подчинительными союзами, например:

Я только-только закончил картину, когда солнце уже готовилось потухнуть.

Бывают сложные предложения, в которых придаточное с главным связаны только по смыслу и разделены знаком препинания, но между ними все еще можно вставить подчинительный союз. Такие предложения называют бессоюзными.

Пример:

На меня нахлынуло осознание: (что) все это время меня обманывали

Значения придаточных предложений в СПП

Придаточные предложения в составе сложных делятся на группы, а далее — на подгруппы по смыслу и виду связи с главным.

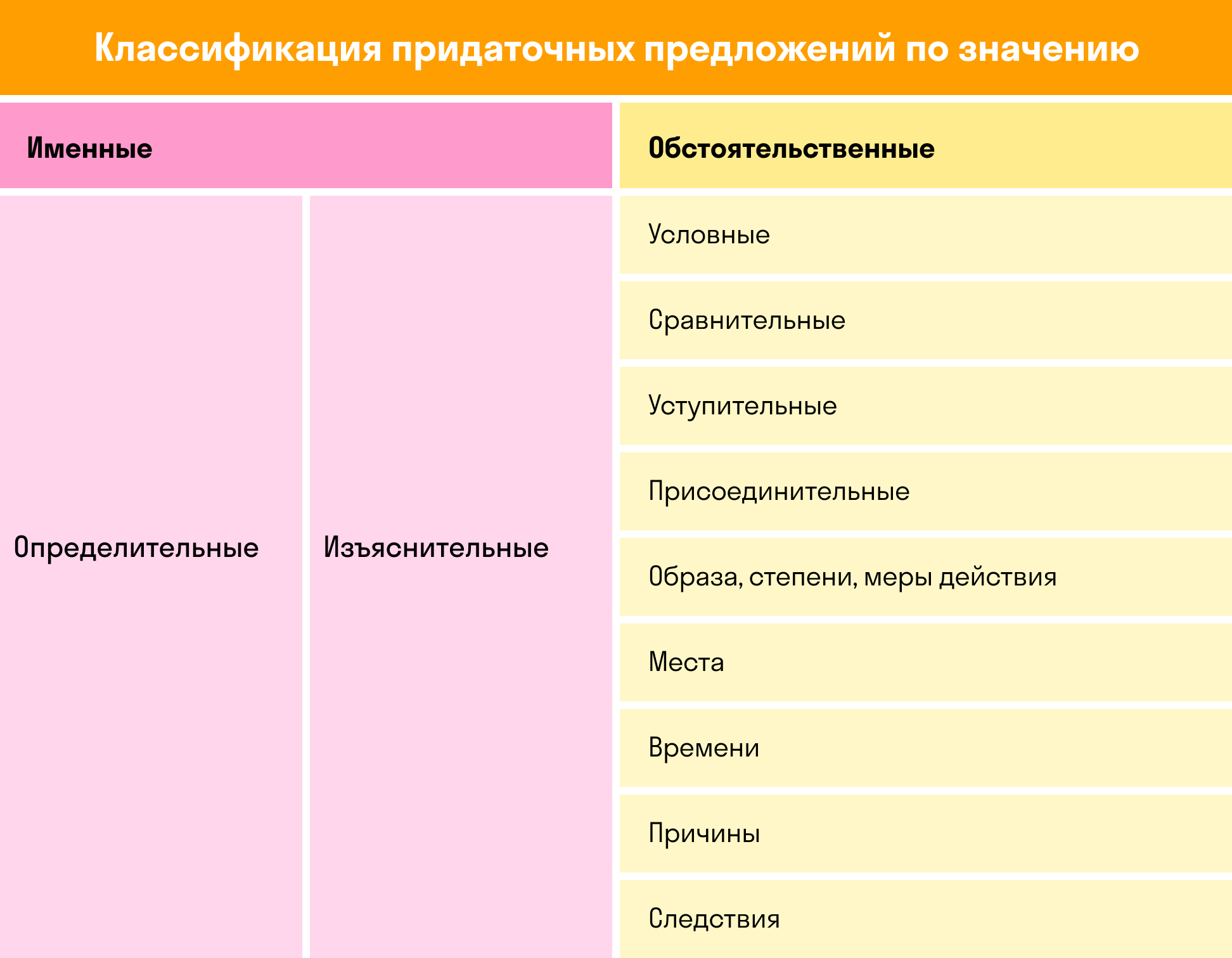
Подробнее о различиях между придаточными в сложном предложении с примерами можно прочесть в этой статье.

Типы подчинения в сложноподчиненном предложении

Иногда в сложноподчиненном предложении не одно, а два и более придаточных. Такой вид сложных предложений называют многочленными. Для них справедливы разные типы подчинения.

Подробнее эту тему мы уже разбирали в статье о сложноподчиненных предложениях.

Знаки препинания в сложноподчиненных предложениях

Между главной и придаточной частями сложного предложения принято ставить запятую. Если одна часть стоит в середине другой, выделять запятой ее нужно с обеих сторон:

• Когда мы вернулись в город, все горести остались за плечами.

• Сейчас, когда мы вернулись в город, все горести остались за плечами.

Если предложения со словами лишь, только, еще и, прежде всего, именно, очевидно, вероятно связаны составным союзом, он разделяется. Тогда перед словом что нужно ставить запятую:

Он согласился лишь потому, что я хорошо попросила.

Если мы выделяем интонацией изъявительные или условные придаточные и ставим их перед главным предложением, между ними ставится тире:

Кто желает — тот получит.

Если по главному предложению понятно, что придаточное его пояснит, нужно ставить двоеточие. То же правило относится и к бессоюзным сложным предложениям:

Он вдруг осознал: дальше не стоит и пытаться.

Задачи на встречное движение

1. Из двух городов одновременно вылетели навстречу друг другу два голубя. Они встретились через 5 ч. Скорость одного голубя 62 км/ч, а второго 68 км/ч. Узнай расстояние между городами.2. Из двух посёлков одновременно выехали навстречу друг другу велосипедист и мотоциклист. Они встретились через 4 ч. Скорость велосипедиста 15 км/ч, а мотоциклиста 57 км/ч. Узнайрасстояние между посёлками.3. От двух пристаней одновременно навстречу друг другу отошли катер и лодка. Они встретились через 6 ч. Скорость лодки 8 км/ч, а скорость катера 35 км/ч. Узнай расстояние между пристанями.4. Две морские звезды одновременно поползли из своих укрытий навстречу друг другу. Первая ползла со скоростью 5 дм/ч, а вторая со скоростью 4 дм/ч. Встретились они через 2 ч. Узнай расстояние между укрытиями морских звёзд. 5. Две девочки вышли одновременно навстречу друг другу из своих домов. Они встретились через 8 мин. Одна шла со скоростью 60 м/мин, а другая со скоростью 70 м/мин. Каково расстояние между домами девочек?6. Два автомобилиста выехали одновременно из двух городов навстречу друг другу. Скорость одного автомобилиста 80 км/ч, а скорость другого 100 км/ч. Узнай расстояние между городами, если автомобилисты встретились через 3 ч.7. Две гремучие змеи выползли одновременно из своих укрытий навстречу друг другу и встретились через 5 мин. Скорость одной змеи 48 м/мин, а скорость другой 53 м/мин. Каково расстояние между укрытиями змей?8. Из двух гнёзд одновременно навстречу друг другу вылетели два ястреба. Встретились они через 6 с. Скорость одного ястреба 6 м/с, скорость другого 16 м/с. Каково расстояние между гнёздами ястребов?9. Из двух городов навстречу друг другу одновременно выехали два мотоциклиста. Встретились они через 4 ч. Скорость одного мотоциклиста 85 км/ч, скорость другого 95 км/ч. Каково расстояние между городами?10. Два пешехода вышли одновременно из двух деревень навстречу друг другу. Один шёл со скоростью 5 км/ч, скорость другого 4 км/ч. Через сколько часов они встретятся, если расстояние между деревнями 36 км?

Счёт в уме

Как тренировать навыки устного счёта, применяя наши примеры?

Практического материала для тренировки счёта в уме в интернете предостаточно. Наши примеры многоразового использования. Каждый пример включает все арифметические действия. Поэтому они наиболее применимы начиная с четвёртого класса. Счёт в пределах сотни. В примерах не действуют математические правила, где первыми надо выполнить умножение и деление, а также действия в скобках.

В каждом примере пять действий, выполняющихся последовательно. Ещё раз – последовательно друг за другом. Например, в выражении 3х7+69-65:5 как идут действия друг за другом, так их и надо выполнять

Вашему ученику трудно выполнить все пять действий? Начинайте с одного. Решите в уме первое действие всех примеров. Потом первые два, три. По мере формирования навыка устного счёта добавляйте по одному действию, и так до пяти. К следующему этапу переходите после качественного освоения предыдущего.

Иногда задают вопрос: а не запомнит ребёнок результаты вычислений? В нашей практике такого не случалось, каждый решался как новый. Примеры разнообразны, действия тоже в разной последовательности.

Тренироваться надо ежедневно по 3-5 минут. Только в этом случае будет результат. Взрослый читает задание, ребёнок старается удержать в памяти на время счёта. Забыл, подскажите. Но не давайте список примеров в руки. Это уже не будет устный счёт.

Соблюдайте технику безопасности. Не заставляйте ребёнка перенапрягаться, работая больше 5 минут. Начало любой тренировки, особенно умственной, требует больших энергетических затрат.

Устойчивый навык устных вычислений у разных ребят требует разного времени для формирования. Следует это помнить.

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

• Единица (1) — самое маленькое число, а самого большого числа не существует.
• Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

• кубические
• уравнение четвёртой степени
• иррациональные и рациональные
• системы линейных алгебраических уравнений

Задачи на движение в обратном направлении

1. Расстояние между городами 504 км. Сколько времени потребуется машине на проезд туда и обратно, если скорость машины в одном направлении 63 км/ч, а в обратном на 21 км/ч больше?2. Расстояние между пристанями в 40 км лодка прошла за 5 ч. На обратном пути её скорость увеличилась на 2 км/ч. За какое время лодка пройдёт весь путь туда и обратно?3. Мальчики прошли до деревни 30 км, двигаясь со скоростью 5 км/ч, а обратно они ехали на велосипеде в 2 раза быстрее. За сколько часов они проехали это расстояние?4. Расстояние между двумя пристанями 45 км. Катамаран прошёл его за 3 ч, на обратном пути его скорость уменьшилась на 6 км/ч. Сколько времени катамаран потратил на путь туда и обратно?5. Расстояние между пристанями 480 км. Катер «Метеор» прошёл его за 6 ч. На обратном пути его скорость увеличилась на 16 км/ч. За какое время катер «Метеор» пройдёт весь путь туда и обратно?6. Божья коровка пролетела до места приземления 3 мин со скоростью 80 см/мин. После этого ей осталось пролететь в 2 раза меньше, и на этот путь она потратила 2 мин. С какой скоростью полетела божья коровка оставшийся путь?7. Путь от города до посёлка, равный 60 км, велосипедист проехал за 4 ч. На обратном пути он уменьшил скорость на 5 км/ч. Сколько времени велосипедист потратил на путь туда и обратно?8. Расстояние между пристанями в 200 км теплоход прошёл за 5 ч. На обратном пути его скорость уменьшилась в 2 раза. За какое время теплоход пройдёт весь путь туда и обратно?9. Баржа проплыла против течения расстояние 84 км за 7 ч, а на обратном пути её скорость увеличилась на 9 км/ч. Сколько времени она потратила на путь туда и обратно?10. Машина шла до остановки 5 ч со скоростью 68 км/ч. После этого ей осталось проехать вдвое меньший путь, на который она потратила 2 ч. С какой скоростью ехала машина после остановки?

Задачи на пропорциональное деление

1. Собрали 640 кг груш и яблок с каждого дерева поровну. Сколько килограммов груш и сколько килограммов яблок собрали, если обработали 7 яблонь и 9 груш?2. В двух книгах 399 страниц. Первую книгу девочка читала 12 дней, а вторую 7 дней, прочитывая каждый день одинаковое количество страниц. Сколько страниц в каждой книге?3. За два дня мастер отремонтировал 28 телевизоров. В первый день он работал 8 ч, а во второй 6 ч. Сколько телевизоров он отремонтировал в каждый из этих дней?4. Купили 84 красных и зелёных перцев и разложили в банки для консервирования: по 4 красных и по 2 зелёных перца в банку. Сколько всего было красных и сколько всего было зелёных перцев? 5. Две бригады работали одинаковое время и заработали вместе 720 руб. Как они должны разделить этот заработок, если в одной бригаде было 5 человек, а в другой 3 человека?6. Сапожник отремонтировал 48 пар обуви за несколько дней: по 2 женские и по 4 мужские пары каждый день. Сколько было отремонтировано мужских и сколько женских пар обуви?7. Девочка сделала несколько венков из незабудок и колокольчиков. В каждом венке было 18 незабудок и 7 колокольчиков. Сколько у неё незабудок и сколько колокольчиков, если общее количество цветков 150?8. В группах детского сада всего 150 детей. В каждой группе по 14 девочек и 16 мальчиков. Сколько девочек и сколько мальчиков в детском саду?9. В нескольких дворах посадили 48 деревьев: по 3 берёзы и 5 лип в каждом дворе. Сколько посадили берёз и сколько лип?10. Для участия в спартакиаде от нескольких школ выделили по 42 бегуна и 24 прыгуна в высоту. Всего было 396 участников. Сколько было бегунов и сколько прыгунов в высоту?

Другие случаи делимости на 4

Рассмотрим случаи, когда нам нужно установить делимость на 4 целого числа, заданного некоторым выражением, значение которого надо вычислить. Для этого мы можем пойти следующим путем:

• представить исходное выражение в виде  произведения нескольких множителей, один из которых будет делиться на 4;
• сделать вывод на основании свойства делимости о том, что все исходное выражение делится на4.

Помочь в решении задачи часто помогает формула бинома Ньютона.

Пример 3

Делится ли на 4 значение выражения 9n-12n+7 при некотором натуральном n?

Решение

Мы можем представить 9 в виде суммы 8+1. Это дает нам возможность применить формулу бинома Ньютона:

9n-12n+7=8+1n-12n+7==Cn·8n+Cn1·8n-1·1+…+Cnn-2·82·1n-2+Cnn-1·8·1n-1+Cnn·1n—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82+n·8+1—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82-4n+8==4·2·8n-1+2·Cn1·8n-2+…+2·Cnn-2·81-n+2

Произведение, которое мы получили в ходе преобразований, содержит множитель 4, а выражение в скобках представляет собой натуральное число. Это значит, что это произведение можно разделить на 4 без остатка.

Мы можем утверждать, что исходное выражение 9n-12n+7 делится на 4 при любом натуральном n.

Ответ: Да.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Также мы можем применить к решению задачи метод математической индукции

Чтобы не отвлекать ваше внимание на второстепенные детали разбора решения, возьмем прежний пример

Пример 4

Докажите, что 9n-12n+7 делится на 4 при любом натуральном n.

Решение

Начнем с установления того, что при значении n=1 значение выражения 9n-12n+7
можно будет разделить на 4 без остатка.

Получаем: 91-12·1+7=4. 4 делится на 4 без остатка.

Теперь мы можем предположить, что при значении n=k значение выражения9n-12n+7 будет делиться на 4. Фактически, мы будем работать с выражением 9k-12k+7, которое должно делиться на 4.

Нам необходимо доказать, что 9n-12n+7 при n=k+1будет делиться на 4 с учетом того, что 9k-12k+7​​​​​ делится на 4:

9k+1-12(k+1)+7=9·9k-12k-5=9·9k-12k+7+96k-68==9·9k-12k+7+4·24k-17

Мы получили сумму, в которой первое слагаемое 9·9k-12k+7 делится на 4 в связи с нашим предположением о том, что 9k-12k+7 делится на 4, а второе слагаемое 4·24k-17 содержит множитель 4, в связи с чем также делится на 4. Это значит, что вся сумма делится на 4.

Ответ: мы доказали, что 9n-12n+7 делится на 4 при любом натуральном значении n методом математической индукции.

Мы можем использовать еще один подход для того, чтобы доказать делимость некоторого выражения на 4. Этот подход предполагает:

• доказательство факта того, что значение данного выражения с переменной n делится на 4 при n=4·m, n=4·m+1, n=4·m+2 и n=4·m+3, где m – целое число;
• вывод о доказанности делимости данного выражения на 4 для любого целого числа n.

Пример 5

Докажите, что значение выражения n·n2+1·n+3·n2+4 при любом целом nделится на 4.

Решение

Если предположить, что n=4·m, получаем:

 4m·4m2+1·4m+3·4m2+4=4m·16m2+1·4m+3·4·4m2+1

Полученное произведение содержит множитель 4, все остальные множители представлены целыми числами. Это дает нам основание предполагать, что все произведение делится на 4.

Если предположить, что n=4·m+1, получаем:

4m+1·4m+12+1·4m+1+3·4m+12+4==(4m·1)+4m+12+1·4m+1·4m+12+4

И опять в произведении, которое мы получили в ходе преобразований,
содержится множитель 4.

Это значит, что выражение делится на 4.

Если предположить, что n=4·m+2, то:

4m+2·4m+22+1·4m+2+3·4m+22+4==2·2m+1·16m2+16m+5·(4m+5)·8·(2m2+2m+1)

Здесь в произведении мы получили множитель 8, который можно без остатка поделить на 4. Это значит, что все произведение делится на 4.

Если предположить, что n=4·m+3, получаем:

4m+3·4m+32+1·4m+3+3·4m+32+4==4m+3·2·8m2+12m+5·2·2m+3·16m2+24m+13==4·4m+3·8m2+12m+5·16m2+24m+13

Произведение содержит множитель 4, значит делится на 4 без остатка.

Ответ: мы доказали, что исходное выражение делится на 4 при любом n.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.

Разрядные единицы обозначают так:

• Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа.
• Десятки — единицами второго разряда и записывают в числе на втором месте справа.
• Сотни — единицами третьего разряда и записывают на третьем месте справа.
• Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
• Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
• Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!

Доказательство признака делимости на 4

Представим любое натуральное число a в виде равенства a=a1·100+a, в котором число a1 – это число a, из записи которого убрали две последние цифры, а число a – это две крайние правые цифры из записи числа a. Если использовать конкретные натуральные числа, то равенство будет иметь вид undefined. Для одно- и двузначных чисел a=a.

Определение 1

Теперь обратимся к свойствам делимости: 

• деление модуля числа a на модуль числа b необходимо и достаточно для того, чтобы целое число a делилось на целое число b;
• если в равенстве a=s+t все члены, кроме одного делятся на некоторое целое число b, то и этот оставшийся член делится на число b.

Теперь, освежив в памяти необходимые свойства делимости, переформулируем доказательство признака делимости на 4 в виде необходимого и достаточного условия делимости на 4.

Теорема 1

Деление двух последних цифр в записи числа a на 4 – это необходимое и достаточное условие для делимости целого числа a на 4.

Доказательство 1

Если предположить, что a=, то теорема в доказательстве не нуждается. Для всех остальных целых чисел a мы будем использовать модуль числа a, который является числом положительным:a=a1·100+a

С учетом того, что произведение a1·100всегда делится на 4, а также с учетом свойств делимости, которые мы привели выше, мы можем сделать следующее утверждение: если число a делится на 4, то и модуль числа a делится на 4, тогда из равенства a=a1·100+a следует, что a делится на 4. Так мы доказали необходимость.

Из равенства a=a1·100+a следует, что модуль a делится на 4. Это значит, что и само число a делится на 4. Так мы доказали достаточность.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

1. Перенести 1 из левой части в правую со знаком минус.

   6х = 19 — 1

2. Выполнить вычитание.

   6х = 18

3. Разделить обе части на общий множитель, то есть 6.

   х = 2

Ответ: х = 2.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.

   5х — 3х — 2х = — 12 — 1 + 15 — 2

3. Приведем подобные члены.

   0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

1. Найти неизвестную переменную.

   х = 1/8 : 4

   х = 1/12

Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Решаем так:

1. 4х + 8 = 6 — 7х
2. 4х + 7х = 6 — 8
3. 11х = −2
4. х = −2 : 11
5. х = — 0, 18

Ответ: — 0,18.

Пример 5. Решить:

Решаем так:

1. 3(3х — 4) = 4 · 7х + 24
2. 9х — 12 = 28х + 24
3. 9х — 28х = 24 + 12
4. -19х = 36
5. х = 36 : (-19)
6. х = — 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

   х — х = 4 — 7

3. Приведем подобные члены.

   0 * х = — 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Решаем так:

1. 2х + 6 = 5 — 7х
2. 2х + 6х = 5 — 7
3. 8х = −2
4. х = −2 : 8
5. х = — 0,25

Ответ: — 0,25.

Математика 4 класс

Варианты контрольных работ:Контрольная работа №1   |   № 2   |   № 3

Задачи по математике для 4 класса:Задачи по математике 4 класс

Олимпиадные задания 4 класс:Олимпиадные задания с ответамиЗадачи олимпиад по математике 4 классШкольная олимпиада 4 класс с решением

Краткая история математики

Академиком А. Н. Колмогоровым предложена такая структура истории математики:
— Период зарождения математики, на протяжении которого был накоплен достаточно большой фактический материал;- Период элементарной математики, начинающийся в VI — V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);- Период математики переменных величин, охватывающий XVII — XVIII века, «который можно условно назвать также периодом „высшей математики“»;- Период современной математики — математики XIX — XX века , в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».

Задачи на движение 4 класс

Задача 1

Грузовик в первый день проехал 600 км, а во второй день 200 км. Весь путь занял 8 часов. Сколько часов в день проезжал грузовик, если он ехал все время с одинаковой скоростью.

Задача 2

Велосипедист проезжает путь из города в поселок, со скоростью 17 км/час, за 5 часов. Сколько времени потребуется пешеходу, что бы пройти этот же путь, если он движется со скоростью 5 км/час?

Задача 3

Автомобиль проехал 400 километров. Двигаясь со скоростью 60 км/час, он проехал за 2 часа первую часть пути. С какой скоростью он двигался остальную часть пути, если он затратил на нее 4 часа?

Задача 4

Скворец летел со скоростью 75 км/час 2 часа. С какой скоростью летит ворона, если такое же расстояние она пролетит за 3 часа?

Задача 5

Автотуристы были в пути 15 часов в течение 2 дней. 420 километров они проехали в первый день и 480 во второй. Сколько часов каждый день они были в пути, если каждый день они двигались с одинаковой скоростью?

Задача 6

От города до поселка 37 километров, а от этого поселка до следующего 83 км. Сколько времени понадобиться, что бы доехать от города до последнего поселка, если двигаться со скоростью 40 км/час?

Задача 7

За 3 часа катер преодолел расстояние в 210 км. Какое расстояние оно пройдет за 5 часов, если его скорость увеличится на 5 км/час?

Задача 8

Теплоход за 9 часов прошел 360 км в первый день. Во второй день теплоход с прежней скоростью был в пути 12 часов. Сколько всего километров преодолел теплоход за 2 дня?

Задача 9

Вертолет пролетает за 4 часа 960 километров. Сколько времени понадобится самолету, чтобы пролететь то же расстояние, если он движется в 2 раз быстрее?

Задачи на движение в одном направлении

Задачи на скорость сближения

Задача 1Решение

40 · 4 = 160 (км)

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

60 — 40 = 20 (км/ч) – это скорость сближения автомобилей

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

160 : 20 = 8 (ч)

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) – расстояние между автомобилями

2) 60 — 40 = 20 (км/ч) – скорость сближения автомобилей

3) 160 : 20 = 8 (ч)

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение:

Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

5 — 4 = 1 (км/ч)

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

5 : 1 = 5 (ч)

Решение задачи по действиям можно записать так:

1) 5 — 4 = 1 (км/ч) – это скорость сближения пешеходов

2) 5 : 1 = 5 (ч)

Ответ: Через 5 часов второй пешеход догонит первого.

Задача 3

Решение:

2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.

Ответ: Задача 4
Решение:

2) 10-6=4 (км/ч) скорость пешехода.

Ответ: Скорость пешехода составляет 4 км/ч.

Задачи на скорость удаления

Задача 1

1. Чему равна скорость удаления между автомобилями?
2. Какое расстояние будет между автомобилями через 3 часа?
3. Через сколько часов расстояние между ними будет 200 км?

Решение:

80 — 40 = 40 (км/ч)

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

40 · 3 = 120 (км)

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

200 : 40 = 5 (ч)

Ответ:

1. Скорость удаления между автомобилями равна 40 км/ч.
2. Через 3 часа между автомобилями будет 120 км.
3. Через 5 часов между автомобилями будет расстояние в 200 км.