Деление многозначных чисел столбиком на двузначное, трехзначное число в 3,4 классе: как объяснить ребенку + топ-10 примеров

Карточка 2

Сосчитай, записывая примеры в столбик.

32+49	37-16
46+24	70-48
83+8	53-38
38+32	45-8

Сосчитай, записывая примеры в столбик.

80-67	45+14
93-48	38+47
59-42	75+8
36-9	68+27

Сосчитай, записывая примеры в столбик.

46+37	80-38
22+58	93-56
59+9	75-9
64+27	87-32

Карточка 7

В летний лагерь приехали дети на двух автобусах. В первом автобусе было 46 детей, а во втором — на 8 детей меньше. Сколько всего детей приехало в школьный лагерь?

3∙7	2∙9	5∙3	9∙0
20:4	70:10	8∙10	32:4
27:3	21:7	7∙4	8∙3

c∙4=12

6∙c=18

27:c=3

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

70-(7∙3)+(8∙4)

Найди значение выражения, решая по действиям.

64-(27+14)+(6∙4)

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

38+(6∙3)-(4∙7)

Карточка 20

На зиму мама закрыла 4 банки вишнёвого варенья, а малинового — в 3 раза больше. Сколько банок малинового варенья закрыла мама? Сколько всего банок закрыла мама на зиму?

Карточка 21

В первый день маляр покрасил 5 скамеек, а во второй — в 4 раза больше. Сколько скамеек покрасил маляр во второй день? Сколько всего скамеек покрасил маляр за два дня?

Карточка 22

Пятачок за неделю съел 3 баночки мёда, в Винни-Пух — в 3 раза больше. Сколько баночек мёда съел Винни-Пух? Сколько баночек мёда они съели вместе?

Карточка 23

Перед домом посадили 4 ели, а берёз — в 3 раза больше. Сколько посадили берёз? Сколько всего деревьев посадили перед домом?

Карточка 24

Денис нарисовал 16 флажков, а Дима — в 4 раза меньше. Сколько флажков нарисовал Дима? Сколько всего флажков нарисовали мальчики?

Карточка 25

Алёна придумала 12 загадок, а Максим — в 2 раза меньше. Сколько загадок придумал Максим? Сколько всего загадок придумали оба мальчика?

Карточка 26

Мастер за день изготовил 24 детали, а его ученик — в 3 раза меньше. Сколько деталей изготовил ученик? Сколько всего деталей они изготовили вместе?

Карточка 28

На первом острове живёт 32 индейца, а на втором — в 4 раза меньше. Сколько индейцев живёт на втором острове? Сколько всего индейцев на двух островах?

Карточка 29

В куске было 54 метра ткани. Из этой ткани сшили 8 курток, расходуя по 3 метра на каждую. Сколько метров ткани осталось в куске?

В театре ученики первого класса заняли в партере 2 ряда по 9 мест и еще 13 мест в амфитеатре. Сколько всего мест заняли ученики первого класса?

Актовый зал освещает 6 люстр по 8 лампочек в каждой, да еще 7 лам­почек над сценой. Сколько всего лампочек освещает актовый зал?

К празднику купили 4 набора шариков по 10 штук в каждом наборе. Лопнули 12 шариков. Сколько шариков осталось на празднике?

В 3 одинаковых наборах 18 карандашей. Сколько карандашей будет в 7 таких наборах?

Начерти таблицу и реши задачу.

Для изготовления 5 одинаковых конструкторов потребовалось 35 деталей. Сколько деталей нужно для изготовления 8 таких конструкторов?

Начерти таблицу и реши задачу.

Крупу разложили на 6 одинаковых упаковок общей массой 12 кг. Сколько упаковок получится из 20 кг?

Начерти таблицу и реши задачу.

В 3 банки для засолки разложили 12 кг помидоров. Сколько банок потребуется для засолки 32 кг помидоров?

Начерти таблицу и реши задачу.

На 32р. купили 4 тетради. Сколько тетрадей можно купить на 56 рублей? на 16 рублей?

Начерти таблицу и реши задачу.

В 2 ведра помещается 16 кг картофеля. Сколько вёдер нужно, чтобы разложить 24 кг картофеля?

Начерти таблицу и реши задачу.

В 4 наборах 32 листа цветной бумаги. Сколько наборов составляют 72 листа бумаги?

Начерти таблицу и реши задачу.

• Начерти прямоугольник со сторонами 8 см и 4 см. Найди его площадь и периметр.
• Сравни:

12 смc1см2мм	7 мc74 дм	9 ммc1 см
14 смc1дм4см	8см7ммc90 мм	100 смc1 м

• Начерти прямоугольник со сторонами 5 см и 4 см. Найди его площадь и периметр.
• Сравни:

14 смc1см4мм	9 мc94 дм	9 ммc1 см
18 смc1дм8см	6см7ммc70 мм	10 смc1 дм

Расставь знаки «+», «-», «·», «: » так, чтобы равенства стали верными.

26*6*7=13	2*2*4=0
7*9*2=18	8*9*2=70
9*9*2=20	8*4*2=30
9*2*2=16	40*5*7=56

Из 12 м ткани портной сшил 6 одинаковых костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

Начерти таблицу и реши задачу.

В огороде собрали 24 кг моркови, редиса — в 4 раза меньше, чем моркови, а чеснока — в 5 раз больше, чем редиса. Сколько килограммов чеснока собрали?

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Начерти таблицу и реши задачу.

Деление в столбик – примеры для тренировки

Без множества примеров трудно освоить технику деления в столбик. Можно перерешать кучу примеров и тогда в любом случае материал усвоится хорошо. Ниже представлен пример деления числа 748 на 2. Давайте разберем этот простой пример деления в столбик.

1. У делимого следует выделить сотни, точнее их 7 у делимого. Для этой цифры подбираем множитель: 2 · 3 = 6 ≤ 7, значит подходит.
2. Пишем 6 под семеркой, а 3 под чертой, это одна из цифр частного.
3. Вычтем из 7 — 6 = 1, и сносим 4. Теперь подбираем множитель: 2 · 7 = 14 = 14 — результат верен. Вторая цифра частного 7.
4. Пишем 14 под 14, и сносим следующую цифру делимого 8. Подбираем множитель: 2 · 4 = 8 = 8, разница 0, число делится без остатка.
5. Итак, результат 374.

Пример деления

Этот пример решен, существует и множество других примеров, которые будут представлены далее по тексту на фото. Эти примеры – готовое решение домашних задач, где подробно расписан процесс деления в столбик, как находится каждая цифра частного. Когда все их перерешаете самостоятельно, то дело доведется до автоматизма и вы сможете решить задание любой сложности, пользуясь своим умением.

Делить в столбик, пожалуй, одна из самых непростых тем в математики. Как уже упоминалось, в процессе используют все четыре действия, (начиная от сложения, заканчивая умножением). Без знаний этих процессов никак не обойтись. Некоторые думают, что зачем знать, как делить, если есть калькуляторы. Но не всегда бывают они под рукой, а посчитать надо сдачи или другую величину, и знания пригодятся на практике. Далее изучите примеры на эту тему.

Пример деленияалгоритмы деления в столбикДеление трехзначного и четырехзначного числаДеление 693 на 3Деление чисел с нулямиДеление без остатка

Еще здесь на портале вы можете узнать много интересного на тему образования вот в этих текстах:

1. Сказка «Репка» по ролям в школе;
2. Сочинение по басне Крылова «Ворона и лисица»;
3. Сочинение на тему «Моя будущая профессия»;
4. Считалки для детей разного возраста;
5. Как правильно писать – на здоровье?

Признаки делимости

Для разбора алгоритма деления 2 значений, которые являются внетабличными (отсутствуют в таблице умножения), необходимо обозначить элементы операции. Пусть дано некоторое выражение v: t = p. Коэффициенты в нем расшифровываются следующим образом:

1. V — делимое, т. е. число, которое требуется разделить.
2. T — математики называют его делителем.
3. P — частное является числовым результатом, который будет получаться при делении двух величин.

Иногда в литературе с физико-математическим уклоном можно встретить такую запись: v / t = p. Кроме того, числа классифицируются на простые и составные. К первой группе относятся все значения, которые делятся без остатка только на 1 или на значение равное исходному, т. е. 23 делится на 1 и на 23, а остальных делителей у него нет вообще. Вторая группа — значения, состоящие из нескольких множителей. Например, 100 = 25 * 4 = 5 * 5 * 2 * 2.

Десятичная система состоит из однозначных цифр, формирующих двузначные, трехзначные, четырехзначные, пятизначные числа (количество разрядов можно продолжать до бесконечности). Для деления двухзначного значения на однозначное без остатка необходимо знать следующие свойства (признаки деления):

1. 0: операция невозможна, поскольку превращает все выражение в пустое множество.
2. 1: делятся все значения.
3. 2: последняя цифра является четным значением, т. е. 0, 2, 4, 6 и 8.
4. 3: сумму цифр, составляющих число, можно разделить на 3. Например, проверить возможность деления 72 на 3. Для этого следует применить такое правило: 7 + 2 = 9. По таблице умножения 9 делится на 3 без остатка. Следовательно, 72 делится на 3.
5. 4: сумма двух цифр делится на 4. Если представлено 5-значное число, то нужно рассматривать 2 последних цифры.
6. 5: последней цифрой является 0 или 5.
7. 6: деление на составные части, т. е. на 2 и 3.
8. 7: возможность выполнения операции определяется по формуле / 7, где а, b и с — соответствуют первой, второй и третьей цифрам. Для двузначной величины — a / 7 и b / 7.
9. 8: должно делиться на 2 и 4. Если количество цифр больше 2, то следует рассматривать делимость без остатка трех последних цифр.
10. 9: деление по таблице умножения. Если число состоит из трех и более цифр, то следует рассматривать деления их суммы на 9.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Пример выполнения деления в столбик

Деление с использованием конкретного примера самая эффективная и распространённая методика в обучении детей делению в столбик. Ученику предлагается разделить трехзначное число, допустим «945» на однозначное число «5» в столбик. В качестве примера лучше брать трехзначное и выше по значению число, чтобы сразу ликвидировать у ребенка страх перед большим числом, которое предстоит делить в столбик.

1 Этап. Школьник должен безошибочно назвать компоненты выражения, которое ему предстоит выполнить. Если все пояснения им усвоены, то ему не составит труда определить «945» как делимое, «5» как делитель, а результат, который будет извлечен после процедуры деления как частное. Чем собственно говоря он сейчас и должен заняться.

2 Этап. Ученика попросить сначала записать в ряд 945 и 5, а затем поделить их с помощью «уголка».

3 Этап. Ребенку предлагается рассмотреть делимое двигаясь слева направо по этому числу и определяя наименьшее число, которое будет больше делителя. Школьник выбирает между числами:9, 94 и 945, соответственно, наименьшим будет число 9. Затем ему надо ответить на вопрос, какое количество раз число 5 поместиться в числе 9? Правильным ответом ученика будет, — один. Соответственно 1 записывается под чертой, и оно станет первой цифрой искомого частного.

4 Этап. Начинается формирование столбика деления. Ребенок должен будет умножить получение число 1 на 5, получив соответственно 5. Результат этой операции записывается под первой цифрой делимого, из числа 9 вычитается 5. Ребенок должен назвать результат и записать его – это число 4.

На этом этапе принципиально важным станет пояснения, что результат вычитания всегда должен получаться меньше делителя, если это не так, значит допущена ошибка при определении какое количество раз число 5 может «поместиться» в числе 9. Естественным будет то, что результат, который будет меньше делителя, должен быть увеличен за счет следующей цифры в ряду делимого. Далее ученик записывает 4 к уже вычисленной четверке.

5 Этап. Дальнейшее объяснение действий лежит в уже знакомой ребенку плоскости математической логики и требует ответа на вопрос о том, — сколько раз число 8 помещается в числе 44? Вспомнив навыки таблицы умножения «наизнанку», ребенок должен дать ответ — это 8. Взрослый поясняет школьнику, что это теперь будет следующая цифра в записи результата частного, которое он продолжает вычислять. Далее следует умножение им 5 на 8 и полученный результат, 40, следует записать под цифрой 44 в столбике.

6 Этап. Здесь операция повторяется и действия обучаемого идут по «накатанному пути». Ребенок вычтет 40 из числа 44, получив 4

Ещё раз взрослому стоит заострить его внимание на том, что 4 меньше делителя 5 и значит действия ребенок выполняет правильно. Предстоит использовать последнюю цифру, оставшуюся у делимого – 5

Дописав ее вниз по столбику к четверке ребенок получит число 45.

Взрослый повторяет вопрос в отношении этого результата. Сколько пятерок в числе 45? Ответом станет число 9, которое и надо записать под чертой.

7 Этап. Завершающий, на нем надо попросить ученика умножить 5 на 9. Школьник должен получить результат 45, озвучив его он делает запись в столбике под цифрой 45. Проделав операцию вычитания 45 из 45 ученик получит 0. При получении этого результата взрослый поясняет школьнику, что им был только что рассмотрен пример деления числа без остатка столбиком.

Как уже всем стало наверно понятно, — ключом к быстрому и эффективному умению делить столбиков для ребенка является его умение пользоваться таблицей умножения. Дальнейшие навыки закрепляются систематическим выполнением примеров и упражнений ребенком сначала под контролем взрослого, а затем уже самостоятельно.

Описание

Программа «Задание на неделю 3 класс» формирует задачи и примеры, которые помогают закрепить ребенку все знания, полученные во третьем классе в течение года, а также подготовится к проверочной и контрольной работе.

На листе формата А4 формируется 13 заданий по математике. При этом задания даются в небольшом объеме, но с максимальным охватом всех типов примеров. Это позволяет детям быстро вспомнить материал 3 класса.

В каждую карточку входят следующие виды заданий:

• задание на повторение понятий «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «множитель», «произведение», «делимое», «делитель» и «частное» с вычислениями;
• примеры на сложение, вычитание, умножение и деление, в том числе: логические (вставить знаки для получения верного равенства),
• выражения на порядок действий (от пяти действий со скобками);
• примеры на умножение и деление разных типов: умножение и деление круглых чисел, внетабличное умножение и деление;
• примеры на деление с остатком с вычисление частного, уменьшаемого или вычитаемого;
• решение уравнений;
• задание на сравнение дробей (долей) и нахождение части от числа;
• задания на повторение единиц измерения длины, массы и времени;
• примеры в столбик: сложение трехзначных чисел, вычитание трехзначных чисел, умножение двухзначного числа на однозначное, умножение трехзначного числа на однозначное и двузначное, на однозначное число;
• примеры на нахождение сторон, периметра и площади квадрата и прямоугольника;
• простые задачи на движение: нахождение скорости, времени или расстояния.

Программа «Задание на неделю 3 класс» написана в Excel с помощью макросов. Данные генерируются случайным образом, что позволяет получить более тысячи вариантов заданий для 3 класса, карточки заданий не повторяются.

Для ознакомления с программой можно скачать изображение карточки, которая получилась с помощью программы. Для получения новой карточки математического диктанта достаточно скачать, нажать на кнопку и распечатать.

Другие программы, которые помогут закрепить навыки счета:

• Цепочки примеров в пределах 1000 (все действия)
• Числовые пирамиды большие (в пределах 50,100 и больше)
• Умножение и деление по типам (табличное, внетабличное, круглых чисел)
• Сложение и вычитание в столбик
• Умножение и деление в столбик
• Деление с остатком на число (с выбором уровня сложности)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий
• Выражения с именованными числами

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным.  Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков. Однозначное — состоит из одного знака. Двузначное — из двух. Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.

• Разряд единиц — то, чем заканчивается любое число.
• Разряд десятков — то, что находится перед разрядом единиц.
• Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

Вычитание — это арифметическое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым. Результат их вычитания — разностью.

Вычитание нуля из числа не изменяет этого числа. a — 0 = a Если из числа вычесть само это число, то разность равна нулю. a — a = 0 Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое. a — (b + c) = a — b — c Чтобы вычесть число из суммы, можно вычесть это число из одного слагаемого и полученную разность прибавить к сумме остальных слагаемых. (a + b) — c = (a — c) + b = a + (b — c) Чтобы прибавить разность к числу, можно прибавить к нему уменьшаемое и из полученной суммы вычесть вычитаемое. а + (b — c) = a + b — c

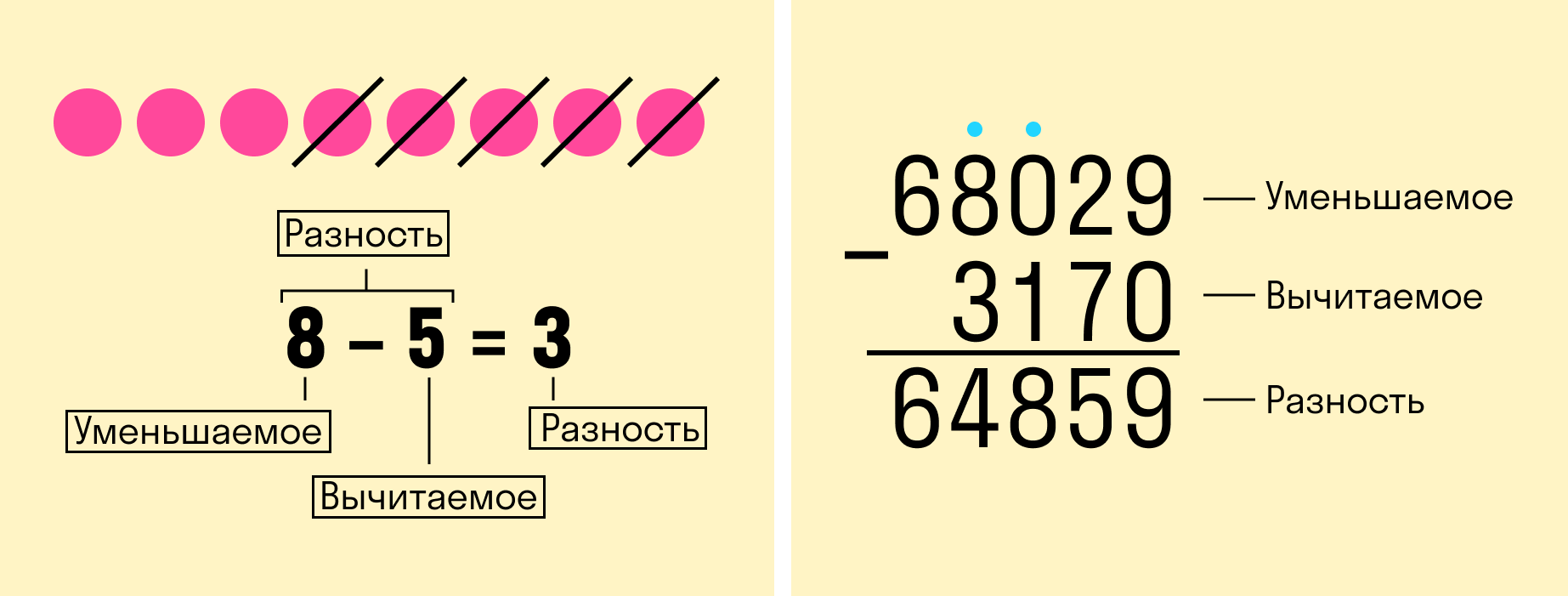
Алгоритм вычитания в столбик

Вычитать столбиком проще, чем считать в уме, особенно при действиях с большими числами. Этот способ наглядный — помогает держать во внимании каждый шаг.

Рассмотрим алгоритм вычитания в столбик на примере: 4312 — 901.

Шаг 1. При вычитании столбиком самое главное — правильно записать исходные данные, чтобы самая правая цифра первого числа была под правой цифрой второго числа.

Большее число (уменьшаемое) записываем сверху. Слева между числами ставим знак минус. Вот так:

Шаг 2. Вычитание столбиком начинаем с самой правой цифры. Вычитаем по цифре (знаку). Результат записываем под чертой.

Шаг 3. Далее вычитаем из второй цифры справа: из «1» ноль.

Шаг 4. Теперь нам нужно вычесть из «3» девять. Это сделать невозможно. Поэтому займем десятку у соседа слева от тройки. Это цифра «4». Поставим над четверкой точку. Занятый десяток прибавим к «3»: 10 + 3 = 13.

Из «13» вычтем девять: 13 − 9 = 4.

Так как мы заняли десяток у «4», значит четверка уменьшилось на единицу. Об этом нам напоминает точка над «4»: 4 − 1 = 3. Вот, как это выглядит:

Рассмотрим пример вычитания в столбик чисел с нулями: 1009 — 423.

Шаг 1. Запишем числа в столбик. Большее число ставим сверху.

Вычитаем справа налево по одной цифре.

Шаг 2. Так как из нуля нельзя вычесть «2», занимаем у соседней цифры слева (ноль). Поставим над «0» точку. У нуля занять нельзя, поэтому смотрим на следующую цифру. Занимаем у «1» и ставим над ней точку. Теперь вычитаем не из нуля двойку, а из «10». Вот так:

Запоминаем!
Если при вычитании столбиком над нулем стоит точка, значит ноль превращается в «9».

Шаг 3. Над нулем стоит точка, поэтому нуль превращается в «9». Вычитаем из «9» четыре: 9 − 4 = 5.

Над «1» стоит точка. Единица уменьшается на «1»: 1 − 1 = 0. Если в результате разности левее всех цифр стоит ноль, то его записывать не надо.

Решение задач с единицами площади

Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.

Задача

В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?

Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.

Решите задачу самостоятельно.

Проверь себя.

S пола = 7 ∙ 8 = 56 (м²)

S лам. = 50 ∙50 = 2 500 (см²)

1 м² = 10 000 см²

10 000 : 2 500 = 4 (шт.) – ламината в 1 м².

56 ∙ 4 = 224 (шт.) – ламината потребуется.

Ответ: 224 штук ламината.

Задача

Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.

Выразим 3 кг в граммах.

1 кг = 1 000 г

3 кг = 3 000 г

35 ∙ 100 = 3 500 (г) – краски потребуется.

3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.

Ответ: 500 г краски не хватит.

Решите аналогичную задачу самостоятельно и проверьте по образцу.

Задача

Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.

Проверь себя.

3 + 4 = 7 (м²) – занимают окно и дверь.

80 – 7 = 73 (м²) – нужно оклеить обоями.

7 ∙ 10 = 70 (м²) – в семи рулонах.

73 – 70  = 3 (м²) – обоев не хватит.

Ответ: не хватит 3 м².

Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».

Решите примеры за одну минуту!

(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =

640 ∙5 ∙0 +640 : 1 – 630 =

? + 150 – 240 – 10 + 26 = 526

Проверь себя.

0, 10, 600.

Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!

В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).

В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными (многозначными) числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Как научиться делить столбиком 4 класс

Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.

Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.

Делитель 8 умножим на  1 и получим —  8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями: