Примеры на деление трехзначных чисел на двузначное, как делить двухзначные на двухзначные с остатком?

Как объяснить деление столбиком

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

• Сначала запишите задачу обычным способом: 250:2=?
• Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
• Затем сделайте сокращенную запись столбиком (уголком):

• Рассуждайте вместе так: сначала найдем неполное частное. Для этого нам потребуется сравнивать первое неполное делимое и делитель. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
• После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Во время объяснения правил деления в столбик желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике.

Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

Деление на двузначное число с остатком

Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.

Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?

А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.

272 : 98    495 : 46    385 : 65   321 : 47

Проверь себя.

Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример

495 : 46

Почему в частном появился 0 (нуль)?

Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.

35 делим на  46. Берем по 0 (35 меньше, чем 46).  Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.

Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?

Давайте вместе решим эту задачу.

430 разделим на 35. Сделаем это столбиком (уголком).

Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.

Разделить можно на черновике, а решение в тетради записать в строчку.

430 : 35 = 12 (ост.10) – башен можно сделать.

Ответ: 12 башен и 10 деталей останется.

Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:

Решите самостоятельно практическую задачу.

Задача

Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?

Проверь себя.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными (многозначными) числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Как делить столбиком меньшее число на большее?

При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.

Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:

• первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
• поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
• когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.

Ниже пример.

Деление столбиком на двузначное число

Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.

Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.

Для начала повторим кратко, как делить столбиком на однозначное число:

А что если деление с остатком? Смотрим в следующем видео:

Как делить столбиком числа с нулями?

улыбчивая девочка у школьной доски

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Как делить столбиком числа с нулями?

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу

В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Делим и умножаем, при помощи таблицы умножения

Здесь стоит объяснить ребенку, про обратное умножению действие, называется «делением». Опираясь на таблицу умножения, покажите обучаемому эту взаимосвязь между делением и умножением на какой-нибудь примере.

Например
: 2 умножить на 4 будет восемь

Здесь акцентируйте внимание на то, что итогом умножения будет произведение двух чисел. Затем будет лучше проиллюстрировать операцию деления, указывая на действие обратной операции умножения

Поделите получившийся ответ «8» на любой множитель – «4» или «2», в результате всегда будет тот множитель, который не использовался в операции.

Также стоит научить распознавать категории, описывающие операции деления, такие как, «делитель», «делимое», «частное»

Важно закрепить данные знания, они наиболее необходимы для дальнейшего процесса обучения!

Определение типа числа

В математике числа делятся на простые и составные. Существует несколько способов определения их принадлежности к тому или иному виду:

1. Автоматизированный.
2. Ручной.

В первом случае применяются специальные таблицы простых чисел, тренажеры или вычислительные машины. Второй является наиболее трудоемким, поскольку нужно рассматривать каждый признак делимости. Если величина делится на 1, на саму себя и какое-либо другое, то является составным. Алгоритм определения простого числа:

1. Выполнить перебор всех делителей.
2. Сделать вывод.

Для примера следует разобрать значение 71

Следует обратить внимание на признаки деления. Новичкам рекомендуется выписать все цифры от 1 до 9

Далее следует возле каждого значения записать результат, поставив знак «+» при делении без остатка или «-» — с остатком:

1. 1: «+».
2. 2: «-» (не является четным).
3. 3: «-» (7 + 1 = 8, 8 не делится на три).
4. 4: «-» (7 и не делятся на 4).
5. 5: «-» (последняя цифра не эквивалентна 0 или 5).
6. 6: «-» (8 не делится на 3, но делится на 2. Этого условия недостаточно).
7. 7: «-» (числа не делятся на 7).
8. 8: «-» (не делится сумма цифр на 2 и 4).
9. 9: отсутствует в таблице умножения на 9.

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным.  Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

рисунок из презентации на тему деления трёхзначного числа столбиком

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

пример деления трехзначного числа на однозначное столбиком

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

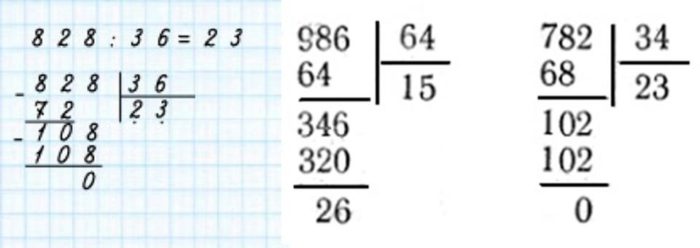
примеры деления столбиком трехзначных чисел на двузначные

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

пример деления в столбик трёхзначного числа на трёхзначное с остатком

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

Описание

Программа «Задание на неделю 3 класс» формирует задачи и примеры, которые помогают закрепить ребенку все знания, полученные во третьем классе в течение года, а также подготовится к проверочной и контрольной работе.

На листе формата А4 формируется 13 заданий по математике. При этом задания даются в небольшом объеме, но с максимальным охватом всех типов примеров. Это позволяет детям быстро вспомнить материал 3 класса.

В каждую карточку входят следующие виды заданий:

• задание на повторение понятий «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «множитель», «произведение», «делимое», «делитель» и «частное» с вычислениями;
• примеры на сложение, вычитание, умножение и деление, в том числе: логические (вставить знаки для получения верного равенства),
• выражения на порядок действий (от пяти действий со скобками);
• примеры на умножение и деление разных типов: умножение и деление круглых чисел, внетабличное умножение и деление;
• примеры на деление с остатком с вычисление частного, уменьшаемого или вычитаемого;
• решение уравнений;
• задание на сравнение дробей (долей) и нахождение части от числа;
• задания на повторение единиц измерения длины, массы и времени;
• примеры в столбик: сложение трехзначных чисел, вычитание трехзначных чисел, умножение двухзначного числа на однозначное, умножение трехзначного числа на однозначное и двузначное, на однозначное число;
• примеры на нахождение сторон, периметра и площади квадрата и прямоугольника;
• простые задачи на движение: нахождение скорости, времени или расстояния.

Программа «Задание на неделю 3 класс» написана в Excel с помощью макросов. Данные генерируются случайным образом, что позволяет получить более тысячи вариантов заданий для 3 класса, карточки заданий не повторяются.

Для ознакомления с программой можно скачать изображение карточки, которая получилась с помощью программы. Для получения новой карточки математического диктанта достаточно скачать, нажать на кнопку и распечатать.

Другие программы, которые помогут закрепить навыки счета:

• Цепочки примеров в пределах 1000 (все действия)
• Числовые пирамиды большие (в пределах 50,100 и больше)
• Умножение и деление по типам (табличное, внетабличное, круглых чисел)
• Сложение и вычитание в столбик
• Умножение и деление в столбик
• Деление с остатком на число (с выбором уровня сложности)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий
• Выражения с именованными числами