Числа

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): axbx = (ab)x.

Пример

52х-4 = 492-х

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

52х-4 = 492-х

52х-4 = 74-2х

52х-4 = (1/7)2х-4

352х-4 = 1

2х — 4 = 0

х = 2

Пример 2

2х-2 = 52-х

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2х-2 = 1/5х-2

Теперь умножим обе части на 52-х и придем к уравнению:

2х-2 × 52-х = 1

10х-2 = 1

10х-2 = 10

х — 2 = 0

х = 2

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

np — q ≤ k ≤ np + p, где q=1−p

Так как np−q = np + p−1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np), то есть когда np + p (а отсюда и np — q) нецелое число, либо два значения, когда np — q целое число.

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Как решаем:

1. По условию дано: n = 730, p = 1/365, g = 364/365
2. np — g = 366/365
3. np + p = 731/365
4. 366/365 ≤ m ≤ 731/365
5. m = 2

Ответ: 2.

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

Как решаем:

В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

x = (2 * 3)/1 = 6

Ответ: x = 6.

Задание 2. Найти неизвестный член: 1/3 = 5/y

Как решаем:

y = (3 * 5)/1 = 15

Ответ: y = 15.

Задача 3. Решить пропорцию: 30/x = 5/8

Как решаем:

x = (30 * 8)/5 = 48

Ответ: x = 48.

Задание 4. Решить: 7/5 = y/10

Как решаем:

y = (7 * 10)/5 = 14

Ответ: y = 14.

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Как решаем:

• Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.

  Получим: 3x = 2y.

• Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.
• После сокращения отношений получилось: x/y = 2/3.

Ответ: 2 к 3.

На следующем примере мы узнаем как составить пропорцию по задаче

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Как решаем:

• Примем всех подписчиков за 100% и запишем условие задачи кратко:

  300 — 100%

  108 — ?%

• Составим пропорцию: 300/108 = 100/x.
• Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

Как решаем:

• Составим пропорцию: 5/2 = x/450.
• Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Как решаем:

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Составим пропорцию:

5 : 100 = х : 98

х = (5 * 98) : 100

х = 4,9

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

• v1 = 75 км/ч
• v2 = 52 км/ч
• t1 = 13 ч
• t2 = х

Как решаем:

1. Составим пропорцию: v1/v2 = t2/t1.

   Соотношения равны, но перевернуты относительно друг друга.

2. Подставим известные значения: 75/52 = t2/13

   t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

1. Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

   30 : 24 = 5 : х

2. Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

   х = 24 * 5 : 30

   х = 4

3. Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Бессоюзные предложения

Если в предложении нет союзов, его части связываются друг с другом знаками препинания:

• запятой,
• точкой с запятой,
• двоеточием,
• тире.

Рассмотрим каждый случай таких ССП на примерах.

Запятая в бессоюзном ССП

Запятая в сложносочиненном бессоюзном предложении нужна, чтобы показать перечисление предметов или событий.

Пример:

Небо стало ясным, звезды скрылись за пеленой утренних облаков.

Точка с запятой в бессоюзном ССП

Точка с запятой в сложносочиненном предложении нужна, когда мы хотим перечислить действия в распространенных предложениях, особенно если в них уже есть запятые.

Пример:

Она схватила сына за плечи, крепко сжала их; он вытер слезы, прижался к матери, что было сил.

Двоеточие в бессоюзном ССП

Когда одна часть сложносочиненного предложения объясняет и дополняет смысл первой, между ними принято ставить двоеточие.

Пример:

Я оглядел полянку: она вся была усыпана одуванчиками.

Тире в бессоюзном ССП

Тире между частями сложносочиненного предложения в русском языке ставят, если в нем по смыслу есть противопоставление или резкое присоединение.

Пример:

Все разом выбежали, похватали сабли — и пошла кутерьма.

Важную роль в вопросе, ставить ли тире между частями предложения с сочинительной связью, играет интонация. Так, тире можно ставить и в назывных предложениях, и в коротких синтаксических конструкциях, если того требует их тон.

Примеры:

• Слышу крик — и вдруг разом тишина.

• Сфотографируйте — и срочно в газету!

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x2 — 2x + 6 = 0
• x2 — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.

2×2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8×2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.

Сложноподчиненное предложение

Сложноподчиненное предложение (СПП) — это вид сложного предложения, в составе которого одно простое предложение по смыслу и интонации подчиняется другому. В этом случае зависимое предложение называется придаточным, а независимое — главным.

Пример сложноподчиненного предложения:

Мне было сложно понять, как ей удалось так быстро привыкнуть к новому городу.

Виды связи в сложноподчиненном предложении

Обычно части СПП в русском языке связаны друг с другом подчинительными союзами, например:

Я только-только закончил картину, когда солнце уже готовилось потухнуть.

Бывают сложные предложения, в которых придаточное с главным связаны только по смыслу и разделены знаком препинания, но между ними все еще можно вставить подчинительный союз. Такие предложения называют бессоюзными.

Пример:

На меня нахлынуло осознание: (что) все это время меня обманывали

Значения придаточных предложений в СПП

Придаточные предложения в составе сложных делятся на группы, а далее — на подгруппы по смыслу и виду связи с главным.

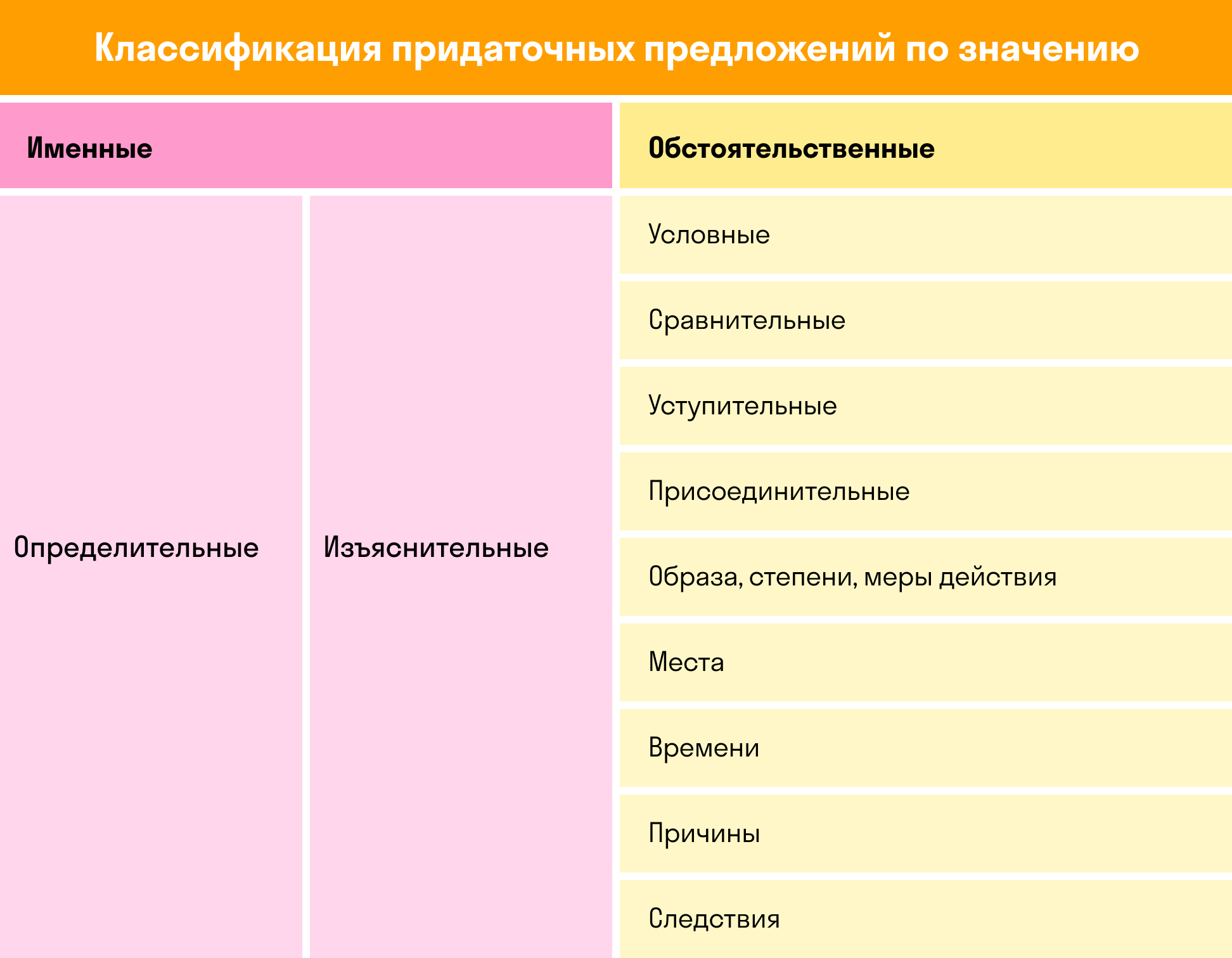
Подробнее о различиях между придаточными в сложном предложении с примерами можно прочесть в этой статье.

Типы подчинения в сложноподчиненном предложении

Иногда в сложноподчиненном предложении не одно, а два и более придаточных. Такой вид сложных предложений называют многочленными. Для них справедливы разные типы подчинения.

Подробнее эту тему мы уже разбирали в статье о сложноподчиненных предложениях.

Знаки препинания в сложноподчиненных предложениях

Между главной и придаточной частями сложного предложения принято ставить запятую. Если одна часть стоит в середине другой, выделять запятой ее нужно с обеих сторон:

• Когда мы вернулись в город, все горести остались за плечами.

• Сейчас, когда мы вернулись в город, все горести остались за плечами.

Если предложения со словами лишь, только, еще и, прежде всего, именно, очевидно, вероятно связаны составным союзом, он разделяется. Тогда перед словом что нужно ставить запятую:

Он согласился лишь потому, что я хорошо попросила.

Если мы выделяем интонацией изъявительные или условные придаточные и ставим их перед главным предложением, между ними ставится тире:

Кто желает — тот получит.

Если по главному предложению понятно, что придаточное его пояснит, нужно ставить двоеточие. То же правило относится и к бессоюзным сложным предложениям:

Он вдруг осознал: дальше не стоит и пытаться.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

1. Перенести 1 из левой части в правую со знаком минус.

   6х = 19 — 1

2. Выполнить вычитание.

   6х = 18

3. Разделить обе части на общий множитель, то есть 6.

   х = 2

Ответ: х = 2.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.

   5х — 3х — 2х = — 12 — 1 + 15 — 2

3. Приведем подобные члены.

   0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

1. Найти неизвестную переменную.

   х = 1/8 : 4

   х = 1/12

Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Решаем так:

1. 4х + 8 = 6 — 7х
2. 4х + 7х = 6 — 8
3. 11х = −2
4. х = −2 : 11
5. х = — 0, 18

Ответ: — 0,18.

Пример 5. Решить:

Решаем так:

1. 3(3х — 4) = 4 · 7х + 24
2. 9х — 12 = 28х + 24
3. 9х — 28х = 24 + 12
4. -19х = 36
5. х = 36 : (-19)
6. х = — 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

   х — х = 4 — 7

3. Приведем подобные члены.

   0 * х = — 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Решаем так:

1. 2х + 6 = 5 — 7х
2. 2х + 6х = 5 — 7
3. 8х = −2
4. х = −2 : 8
5. х = — 0,25

Ответ: — 0,25.

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

Как решаем:

1. A — встреча с другом состоится, х и у — время прихода. Значит:
   0 ≤ х, у ≤ 60.
2. В прямоугольной системе координат этому условию удовлетворяют точки, которые лежат внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть: 
   y−x < 5, y > x
   x−y < 5, x > y.
3. Этим неравенствам удовлетворяют точки из области G — то, что выделено красным:
4. Тогда вероятность встречи равна отношению площадей области G и квадрата:
   P(A)=S_G/S_OABC= 60 * 60 — 55 * 5560 * 60 = 23144 = 0,16

Ответ: 0,16

У нас есть отличное онлайн обучение по математике для учеников с 1 по 11 классы, записывайся на пробное занятие!

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

1. Найдем наименьшее общее кратное для определения единого делителя.

   Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

   НОК (15, 18) = 3 * 2 * 3 * 5 = 90

2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

   90 : 15 = 6,

   90 : 18 = 5.

   Полученные числа запишем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
   • если делимое больше делителя, нужно преобразовать в смешанное число;
   • если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.
2. Сложить дробные части.

   Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

3. Суммировать полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Существительное с предлогом «на пример»

Учитель указал на пример, приведенный в энциклопедии.

Зададим вопрос: указал на что? На пример.

«Пример» в данном случае – дополнение, выраженное именем существительным. Глагол-сказуемое управляет дополнением в форме винительного падежа единственного числа. Раздельное написание существительного с предлогом можно доказать при помощи падежного вопроса или определения между ними:

• на какой? при­мер;
• на чей? при­мер;
• на хоро­ший при­мер;
• на ваш при­мер.

Примеры предложений

Посмотрите на пример с составленным уравнением.
Мы смотрим на пример брата.
В новых исследованиях мы всегда опираемся на пример предшественников.
Обратим внимание на пример из статистики.
Посмотрим на пример схемы и составим похожую.
Глядя на пример, изображенный на рисунке, мы понимаем, как устроена растительная клетка.
Мы сделали вывод, сославшись на пример из проверенного источника.
Посмотрев на пример наставника, в успехе он не сомневался.

Фрагмент текста

Многие сочинения пишутся по работам талантливого филолога и культуролога Д. С. Лихачева. В его сборнике «Письма о добром и прекрасном» приведены тексты на разные темы. В них автор поднимает важные проблемы и делится собственными мыслями.

Для написания сочинения «Легко ли быть молодым» используют второе письмо «Молодость — вся жизнь». Текст начинается с того, что автор высказывает предположение: «Взрослая жизнь будет в другой обстановке и с иными людьми». Он считал, что школа и университет — это этапы, которые быстро забываются и не имеют большого значения.

Но со временем Лихачев понял, что настоящие друзья остались с молодости. Подобная история произошла и с его родителями, знакомыми. Автор заметил, что с возрастом обретать истинную дружбу тяжело

Поэтому важно относиться бережно к молодости, не тратить время зря

По мнению Лихачева, именно в юности человек приобретает самостоятельный опыт жизни, получает разные навыки и умения. В это время нужно приучать себя к труду, иначе есть риск остаться ленивым и инфантильным.

На основе этого фрагмента школьнику нужно написать сочинение-рассуждение «Легко ли быть молодым».

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6
• 21,10200000 = 21,102

Основные свойства
Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Основные свойства Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Карточка 2

Сосчитай, записывая примеры в столбик.

32+49	37-16
46+24	70-48
83+8	53-38
38+32	45-8

Сосчитай, записывая примеры в столбик.

80-67	45+14
93-48	38+47
59-42	75+8
36-9	68+27

Сосчитай, записывая примеры в столбик.

46+37	80-38
22+58	93-56
59+9	75-9
64+27	87-32

Карточка 7

В летний лагерь приехали дети на двух автобусах. В первом автобусе было 46 детей, а во втором — на 8 детей меньше. Сколько всего детей приехало в школьный лагерь?

3∙7	2∙9	5∙3	9∙0
20:4	70:10	8∙10	32:4
27:3	21:7	7∙4	8∙3

c∙4=12

6∙c=18

27:c=3

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

70-(7∙3)+(8∙4)

Найди значение выражения, решая по действиям.

64-(27+14)+(6∙4)

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

38+(6∙3)-(4∙7)

Карточка 20

На зиму мама закрыла 4 банки вишнёвого варенья, а малинового — в 3 раза больше. Сколько банок малинового варенья закрыла мама? Сколько всего банок закрыла мама на зиму?

Карточка 21

В первый день маляр покрасил 5 скамеек, а во второй — в 4 раза больше. Сколько скамеек покрасил маляр во второй день? Сколько всего скамеек покрасил маляр за два дня?

Карточка 22

Пятачок за неделю съел 3 баночки мёда, в Винни-Пух — в 3 раза больше. Сколько баночек мёда съел Винни-Пух? Сколько баночек мёда они съели вместе?

Карточка 23

Перед домом посадили 4 ели, а берёз — в 3 раза больше. Сколько посадили берёз? Сколько всего деревьев посадили перед домом?

Карточка 24

Денис нарисовал 16 флажков, а Дима — в 4 раза меньше. Сколько флажков нарисовал Дима? Сколько всего флажков нарисовали мальчики?

Карточка 25

Алёна придумала 12 загадок, а Максим — в 2 раза меньше. Сколько загадок придумал Максим? Сколько всего загадок придумали оба мальчика?

Карточка 26

Мастер за день изготовил 24 детали, а его ученик — в 3 раза меньше. Сколько деталей изготовил ученик? Сколько всего деталей они изготовили вместе?

Карточка 28

На первом острове живёт 32 индейца, а на втором — в 4 раза меньше. Сколько индейцев живёт на втором острове? Сколько всего индейцев на двух островах?

Карточка 29

В куске было 54 метра ткани. Из этой ткани сшили 8 курток, расходуя по 3 метра на каждую. Сколько метров ткани осталось в куске?

В театре ученики первого класса заняли в партере 2 ряда по 9 мест и еще 13 мест в амфитеатре. Сколько всего мест заняли ученики первого класса?

Актовый зал освещает 6 люстр по 8 лампочек в каждой, да еще 7 лам­почек над сценой. Сколько всего лампочек освещает актовый зал?

К празднику купили 4 набора шариков по 10 штук в каждом наборе. Лопнули 12 шариков. Сколько шариков осталось на празднике?

В 3 одинаковых наборах 18 карандашей. Сколько карандашей будет в 7 таких наборах?

Начерти таблицу и реши задачу.

Для изготовления 5 одинаковых конструкторов потребовалось 35 деталей. Сколько деталей нужно для изготовления 8 таких конструкторов?

Начерти таблицу и реши задачу.

Крупу разложили на 6 одинаковых упаковок общей массой 12 кг. Сколько упаковок получится из 20 кг?

Начерти таблицу и реши задачу.

В 3 банки для засолки разложили 12 кг помидоров. Сколько банок потребуется для засолки 32 кг помидоров?

Начерти таблицу и реши задачу.

На 32р. купили 4 тетради. Сколько тетрадей можно купить на 56 рублей? на 16 рублей?

Начерти таблицу и реши задачу.

В 2 ведра помещается 16 кг картофеля. Сколько вёдер нужно, чтобы разложить 24 кг картофеля?

Начерти таблицу и реши задачу.

В 4 наборах 32 листа цветной бумаги. Сколько наборов составляют 72 листа бумаги?

Начерти таблицу и реши задачу.

• Начерти прямоугольник со сторонами 8 см и 4 см. Найди его площадь и периметр.
• Сравни:

12 смc1см2мм	7 мc74 дм	9 ммc1 см
14 смc1дм4см	8см7ммc90 мм	100 смc1 м

• Начерти прямоугольник со сторонами 5 см и 4 см. Найди его площадь и периметр.
• Сравни:

14 смc1см4мм	9 мc94 дм	9 ммc1 см
18 смc1дм8см	6см7ммc70 мм	10 смc1 дм

Расставь знаки «+», «-», «·», «: » так, чтобы равенства стали верными.

26*6*7=13	2*2*4=0
7*9*2=18	8*9*2=70
9*9*2=20	8*4*2=30
9*2*2=16	40*5*7=56

Из 12 м ткани портной сшил 6 одинаковых костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

Начерти таблицу и реши задачу.

В огороде собрали 24 кг моркови, редиса — в 4 раза меньше, чем моркови, а чеснока — в 5 раз больше, чем редиса. Сколько килограммов чеснока собрали?

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Начерти таблицу и реши задачу.

Сочинение №1

Тема: «Какую книгу я считаю величайшим достижением культуры», направление: «Книга (музыка, спектакль, фильм) про меня»

(Автор сочинения – Гончарова Алина Николаевна)

Наверное, каждый человек хоть раз задумывался над тем, какую книгу он считает величайшим достижением культуры. Так, с раннего возраста ребенок познает мир с помощью книг. Родители читают сказки, стихи, были, и нам кажется, что лучше этих произведений нет. Но это не так. Когда мы вырастаем, то по-другому смотрим на мир, понимаем, какие книги оказывают на нас наибольшее эмоциональное воздействие. Я только с четырнадцатилетнего возраста начала осознанно читать и анализировать книги. И если после прочтения произведения и смогла найти ответы на вопросы, то данную книгу я считаю великой.

Размышляя о великой книге, я не могу не братиться к произведению Льва Николаевича Толстого «Война и мир», в котором поднимается множество актуальных проблем.Одна из них – поиск смысла жизни. Главный герой, Андрей Болконский, ищет свое предназначение в жизни. Так, в салоне у Анны Павловны Шерер о понимает, что ему неинтересна свеская жизнь, пустые разговоры войне. Но чего же тогда хочет Андрей? Он жаждит славы. Чтобы стать наменитым , он отправляется на войну с целью наград и званий. Война готовила герою другую историю. В битве при Аустерлице Болконский был тяжело ранен, истекая кровью, он смотрел на небо, плывущие облака и понимал, что нужно что-то зменить в своей жизни.

После сражения Андрей переосмысливает жизнь. Герой винит себя в смерти жены, но решает не опускать руки и заботиться о своей семье . Андрей Болконский впадает в депрессию. И только юная девушка , Наташа Ростова, смогла вернуть его к жизни. Благодаря ей, он понимает, что такое настоящая любовь. Беззаботность, привлекательность девушки заставляют Андрея жить. Он хочет вместе с Наташей создать семью, воспитывать своего ребенка. Узнав об этом, отец героя отправляет его в армию . Правильно ли поступил Андрей, уехав в армию? Однозначного ответа никто дать не может. Ведь в то время нельзя было ослушаться отца и нужно было ехать. Но и молодую девушку опасно оставлять одну на долгое время, потому что вокруг много соблазнов. Когда Наташа изменила Андрею, он не смог ее сразу простить, хотя все равно любил. Смысл жизни героя заключался в служении Родине. Жаль, что герой не сразу понял, чего он хочет от жизни. Что не нужна ему слава, всеобщее признание, а верное служение Отечеству и тихая жизнь рядом с любимым человеком.

Таким образом, величайшим достижением культуры я считаю роман Л.Н. Толстого «Война и мир». К даннму произведению хочется возвращаться вновь и вновь, так как там отражены главные проблемы человечества. Когда возникает какой-либо вопрос, то ответ на него всегда можно найти в данном романе. И я знаю, что еще неоднократно вернусь к прочтению данного памятника культуры.

1. Соответствие теме зачёт
2. Аргументация. Привлечение литературного материала. зачёт
3. Композиция и логика рассуждения. незачёт
4. Качество письменной речи. зачёт
5. Грамотность. зачёт

ИТОГ: зачёт

Рекомендации

P.S. Алина! Работа неплохая, но при прочтении возникает впечатление, что она самостоятельна на 50%, словно писали два разных человека. Роман «Война и мир» — это масштабное произведение, в котором именно на примере Андрея Болконского можно было показать становление как главного героя, так и то, какое влияние он своими поступками оказал на Вас. А в этой работе просматривается поверхностное прочтение романа. Старайтесь внимательнее читать произведения, привлекая больше фрагментов произведения для более детального анализа. Удачи и терпения!

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит 2,5 * 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Сложение и умножение вероятностей

Немного теории:

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂,…, A_n образуют полную группу несовместных событий, то справедливо равенство: 

P(A1) + P(A2) + … + P(An) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

Как рассуждаем:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Понятие предложения

Предложение — это синтаксическая единица, которая выражает законченную мысль. Может быть простым или сложным.

Три типа предложений по цели высказывания:

• повествовательное (сообщение);

• вопросительное (вопрос, проблема);

• побудительное (совет).

Предложение состоит из слов или словосочетаний, которые объединены по смыслу и грамматически. У каждого есть грамматическая основа — подлежащее и/или сказуемое.

Простые предложения — это такие предложения, в которых есть одна грамматическая основа.

Сложные предложения — это такие предложения, у которых есть две или более грамматических основ.

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Скачать

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8

б) 9 + 11 + 2

в) 30 + 0 + 13

Как решаем:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2

б) 18 — 1 — 4

в) 55 — 55

Как решаем:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

в) 55 — 55 = 0

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9

б) 16 + (4 — 3) + 7

в) 0 + 2 + 4 — 0

Как решаем:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

в) 0 + 2 + 4 — 0 = 2 + 4 = 6