Быстро подготовиться к базовой математике
Содержание:
Задание 6 (Делаем обязательно!)
Проверяется
ваше умение разделить случаи, когда требуется округлить величину в большую
сторону, а когда — в меньшую.
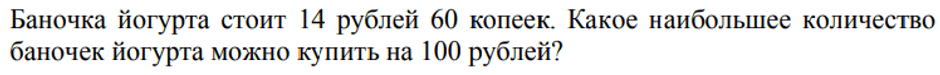
Если
ходите в магазин с карманными деньгами, то сталкиваетесь с подобными задачами
каждый день! Разделим 100 рублей на стоимость одной упаковки йогурта. Не
забываем приводить все величины к одной размерности:
100 : 14,6 = 6, 849…
Так сколько баночек йогурта вам продадут? На 7 штук
вам явно не хватает денег, значит округлить полученную величину надо до целого
в меньшую сторону. Математическое правило округление в этой задаче не
поможет.
Ответ: 6.

Одна пачка на 6 рулонов, значит на 63 рулона:
63 : 6 = 10,5
Но опять же, никто полпачки вам не продаст. Включаем
логику: возьмем меньше — не хватит еще половины пачки на 3 последние рулона.
Значит округлить надо в большую сторону, взять клей с небольшим запасом.
Снова математическое правило округления игнорируем.
Ответ: 11.
Задание 10 (Делаем обязательно!)
Простая задача на определение вероятности.
Решаем с помощью формулы:
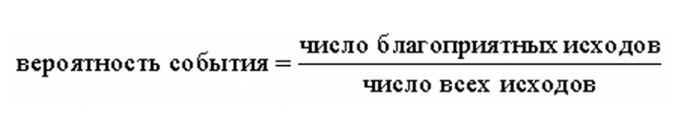

Внимательно читаем вопрос: спрашивают вероятность купить исправную
лампочку. Если из ста 3 неисправны, значит остальные в порядке, и нам подойдет
любая из оставшихся 97 штук. Это и есть наши благоприятные исходы из формулы.
Ответ: 0,97.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит ответ
у вас выйдет некрасивый, но вы его «причЕшите» округлением.
Еще один подвох: формулировка с предлогом «на». К примеру, «на 100
лампочек 3 неисправны, найдите вероятность купить неисправную». Подходящие
исходы даны тут явно: 3 неисправные лампочки. А вот число всех исходов спрятано
и составляет 103, потому что «на».
Всегда есть вероятность, что вам не повезет, и попадется задачка с
перебором подходящих вариантов… Тема довольно объемная, можете изучить ее
самостоятельно или надеяться на удачу.
Задание 19
Чем дальше, тем интереснее становятся задачи. Этот номер уже напоминает олимпиадную задачку, правда для средней школы.
Если хотите сдать базовую математику и решить 19 номер, надо немного познакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте, если время на ЕГЭ позволяет.

Например,
тут нам помогут признаки делимости. Отдельного признака для 12 нет, потому нам
надо разложить его на разные множители, признак для которых есть.
Например, это:
- 3: чтобы
число делилось на 3, надо, чтобы сумма его цифр делилась на 3; - 4: чтобы
число делилось на 4, надо, чтобы число, образованное последними двумя цифрами,
делилось на 4.
Начнем
с признака для четырех. Пока что наше число заканчивается на 13. На 4 не
делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на
61. Тоже не подходит. Вычеркнем еще одну. Теперь на конце 76… Вот оно! От
изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать
одну.
Теперь
проверим признак для трех: 7+5+1+5+7+6 = 31. Какое ближайшее число разделиться
на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576. Конечно, это не единственное решение.

А
задание такого типа можно попытаться подобрать, расположений не слишком много.
Мы все же постараемся порассуждать, чтобы уменьшить количество возможных
вариантов.
Чтобы
число делилось на 10, оно должно заканчиваться на 0. Например, это получится,
если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под
условие задачи подойдет 7 + 27 + 356 = 390.
Ответ:
390.
Задание 1 (Делаем обязательно!)
Задание проверяет базовые навыки счета, которым вы научились в 5-6 классах. Для получения балла надо:
- Уметь
выполнять арифметические действия с простыми и десятичными дробями, - Правильно
расставлять порядок действий, - Быть
предельно внимательным.
Уделите
пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления
простых и десятичных дробей. Мы лично знаем ребят, которые не могут правильно
разделить десятичные дроби в 11 классе!
Задание 2
(Делаем обязательно!)
Задача чуть сложнее: пример со степенями. Для выполнения надо:
Выучить формулы свойств степеней
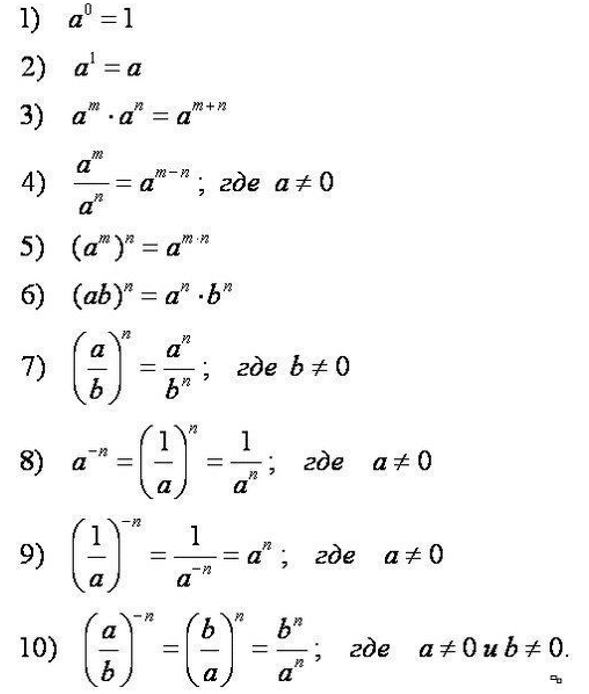
Это формулы свойств степеней
- Научиться их корректно применять,
- Включить еще больше внимательности, чем в первом номере.
Нужная теория будет в справочных материалах на экзамене, но это не поможет, если не наработан навык ею пользоваться. Практика обязательна.
Задание 3
Составители экзамена проверяют ваш навык работы с процентами. Задачи на проценты бывают трех типов:
Тип 1. Найти часть от числа
Часть
может быть выражена в процентах или сразу в виде дроби. Например, придется
искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте
специфику задачи: нам известно целое — вся зарплата до вычета налога. А
работать мы будем с кусочком — 13-ю процентами. Сколько это в рублях нам еще
предстоит узнать.
Чтобы ответить на вопрос задачи, делаем 3 шага:
А.
Переводим процент в десятичную дробь
Для
этого всегда надо количество процентов поделить на 100.
13 : 100 = 0,13
Б.
Находим, сколько это от зарплаты в рублях
12 500 * 0,13 = 1 625 (р.) —
налог, который удержат с зарплаты Ивана Кузьмича.
В.
Отвечаем на вопрос задачи
У
нас просили зарплату после вычета налога, а не сам налог.
12 500 — 1625 = 10 875 (р.)
Ответ:
10 875.
Будьте внимательны, многие завалятся именно на последнем шаге!
Тип 2. Найти число по его части
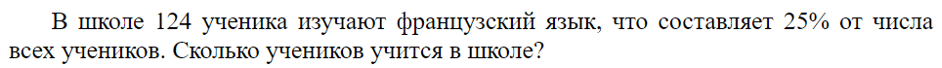
Прочувствуйте
разницу с прошлой задачей: тут 124 это и есть 25%, то есть одна и та же
величина выражена в процентах и в абсолютных величинах, в данном случае — в
учениках. Просят узнать целое — 100%.
А.
Переводим процент в десятичную дробь
25 : 100 = 0,25
Б.
Находим, сколько учеников всего
124 : 0,25 = 496 (у.) — всего.
Ответ: 496.
Тип 3. Найти, сколько процентов часть составляет от целого

Особенность
подобных заданий — не дано процентов, есть только абсолютные величины. В данном
случае — стоимость футболки в рублях.
А.
Находим, какую долю новая цена составляет от первоначальной
680 : 800 = 0,85
Б. Переводим долю в процент
В прошлых задачах мы уже дважды выполнили обратное
действие. В этот раз сделаем наоборот: умножим полученную дробь на 100
0,85 * 100 = 85 % — столько процентов
новая цена составляет от старой
В. Отвечаем на вопрос задачи
Нас спросили, на сколько процентов цена снизилась, что
стала 85% от первоначальной? Конечно, изначально она была 100%. Итого
100 — 85 = 15%.
Ответ:
15%
Остался последний тип, не так явно связанный с
процентами…
Тип 4. Задачи на соотношение
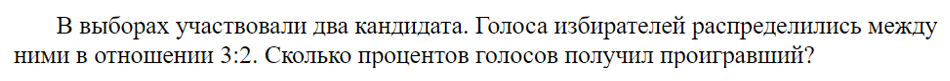
Если чуть перефразировать условие, то за первого
кандидата проголосовали 3 части избирателей, а за второго — 2 части.
Особенность этих частей в том, что они ОДИНАКОВЫЕ по величине.
Если одна будет состоять из 10 человек, то за первого
кандидата будет 30, а за второго — 20.
А. Считаем общее количество частей
3 + 2 = 5
Б. Узнаем, сколько голосов составляет одна такая часть
Тут речь о процентах проголосовавших. Сколько всего
проголосовало? Конечно, 100%! Значит каждая из пяти частей «весит»…
100 : 5 = 20%
В.
Отвечаем на вопрос задачи
За
проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
20 * 2 = 40%
Ответ:
40%.
Решение этих задач удобнее всего оформить табличкой
| 1 кандидат | 2 кандидат | Всего | |
| Части | 3 | 2 | 5 |
| Абсолютные величины | 20% * 2= 40% | 100 % |
1 часть = 100% : 5 = 20%
Если рассчитываете решать текстовую задачу, включите здравый смысл! Ответ всегда можно проверить на адекватность благодаря обычной логике. Без нее и выстроить ход решения выйдет вряд ли.
Задание 18 (Делаем обязательно!)
Задача проверяет у ребят, которые хотят сдать базовую математику, умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все,
что от вас требуется – схематично изобразить на черновике ясень, рябину и
осину, указать известную разницу в высоте и внимательно сопоставить картинку с
утверждениями.
Ответ:
14
Важно! Не
додумывайте какие-то дополнительные условия, не указанные в тексте задачи.
Учитесь читать строго то, что написано. А
бывают случаи, когда с визуализацией задачки придется постараться
А
бывают случаи, когда с визуализацией задачки придется постараться.

Тут
иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет
наглядно изобразить множество объектов. В данном случае — школьников. Давайте
прикинем, как ребята могут распределиться по кружкам?
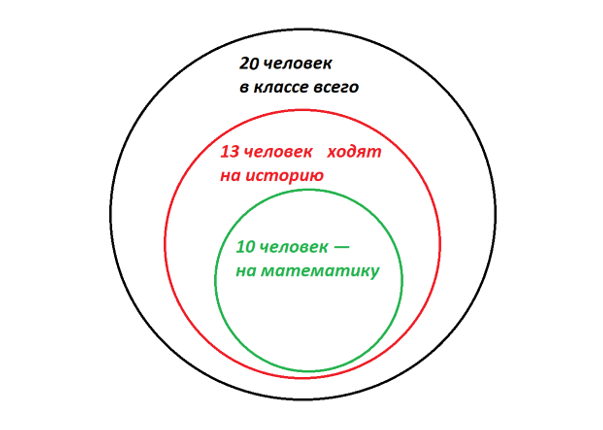
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем, 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.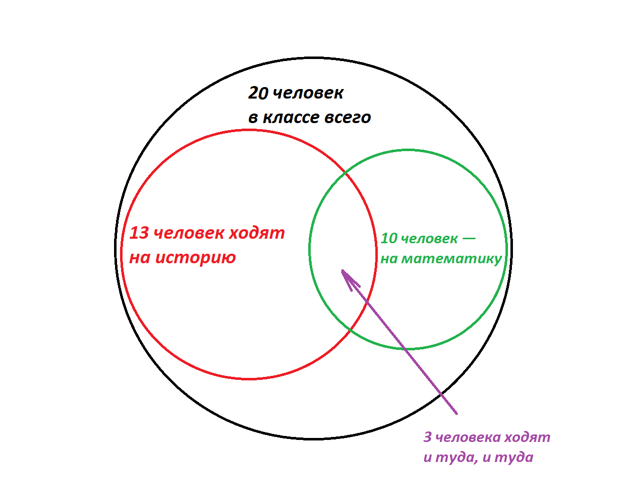
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.
Конечно, возможны еще какие-то промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
- Смотрим на первую картинку. Даже если все ребята будут
очень стараться посетить оба кружка, они ограничены условиями задачи, и
максимум на оба попадут 10 человек из 20. НЕТ. - Тут надо рассмотреть другую крайность, которую мы
изобразили на второй картинке. Как бы ребята не старались не встречаться на
кружках, хотя бы трое попадут на оба сразу. ДА. - Уж точно неверно. На обеих наших картинках есть
ребята, которые ходят на историю, но не ходят на математику. НЕТ. - Смотрим на первую картинку. Максимум оба кружка могут
посещать 10 человек. ДА.
Ответ: 24.
Так что для решения иногда мало логики, понадобится
еще чуток воображения. Потренируйтесь, и ваши шансы получить балл повысятся.