Как доступно объяснить ребёнку суть деления чисел

Деление на двузначное число с остатком

Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.

Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?

А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.

272 : 98    495 : 46    385 : 65   321 : 47

Проверь себя.

Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример

495 : 46

Почему в частном появился 0 (нуль)?

Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.

35 делим на  46. Берем по 0 (35 меньше, чем 46).  Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.

Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?

Давайте вместе решим эту задачу.

430 разделим на 35. Сделаем это столбиком (уголком).

Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.

Разделить можно на черновике, а решение в тетради записать в строчку.

430 : 35 = 12 (ост.10) – башен можно сделать.

Ответ: 12 башен и 10 деталей останется.

Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:

Решите самостоятельно практическую задачу.

Задача

Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?

Проверь себя.

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Тема: деление вида 87 : 29

Предварительный просмотр:

Тема: деление вида 87 : 29

Тип урока: изучение нового материала.

Место урока: первый урок.

Оборудование: карточки с заданием.

Цель: научиться решать деление двузначного числа на двузначное.

Ожидаемый результат: решает примеры на деление способом подбора.

1. Образовательная:

учить делить двузначное число на двузначное методом подбора;

1. Развивающая:

• развивать вычислительные навыки, познавательный интерес, умение рассуждать;
• творческие способности посредством заданий на приемы умственных действий;

1. Воспитательная:

воспитывать эстетический вкус, аккуратность при работе в тетради, толерантность.

1. Организационный момент. Концепция внимания.

– Ребята, посмотрите, кто у нас сегодня в гостях? (Знайка-Математик.)

– Знайка-Математик снова у нас на уроке.

Прозвенел долгожданный звонок.Знайка с нетерпением встречи с вами ждёт.

(Учитель показывает геометрические фигуры разного цвета (6). В течение 1 минуты учащиеся запоминают фигуры. Затем дети закрывают глаза, а учитель в это время меняет одну фигуру на другую. Дети должны написать, какая фигура пропала, а какая появилась. Затем учитель меняет 1 фигуру красного цвета на синий, а дети должны написать, какого цвета не стало и какой появился).

II. Сообщение темы и целей урока.

Сегодня тема новая у нас. И Знайка-математик пришел в наш класс, Чтоб научить нас быстро вычислять, Делить, в ответе цифру подбирать.

III. Устный счет.

Давайте, ребята, учиться считать,Делить, умножать, прибавлять, вычитать.Запомните все, что без точного счетаНе сдвинется с места любая работа.

Без счета не будет на улице света,Без счета не может подняться ракета,Без счета письмо не найдет адресата,И в прятки сыграть не сумеют ребята.

Считайте, ребята, точнее считайте,Хорошее дело смелей прибавляйте,Плохие дела поскорей вычитайте.Учебник научит вас точному счёту.

Скорей за работу, скорей за работу.

— Какие устные счеты принес нам Знайка – математик?

1. Подберите такое число, чтобы от умножения его на 16 получить 48.
2. Прочитайте только те, которые делятся на 5, на 8, на 9.36, 40, 6, 15, 0, 72, 45
3. На передних лапках у белки по 4 пальца, а на задних по 5. Сколько всего пальцев на лапках у белки?

IV. Работа над новой темой.

1. Выполните умножение 14 x 7 и составьте все примеры на умножение и деление из данной тройки чисел.14 x 7= 987 x 14= 98 (от перестановки множителей произведение не меняется)98 : 14=798 : 7=14— Используя взаимосвязь умножения и деления, объясните, как разделить 98 на 14 (Надо найти число, которое бы при умножении на 14 давало бы 98).Найдем число, на которое надо умножить 14. Пробуем число 2, проверяем 14 x 2=28, 28.Проверяем число 4: 14 x 4=5614 x 5=7014 x 6=8414 х 7=98Значит 98 : 14=7
2. Читаем в учебнике новый материал, с.18
3. №1 с.18 – решаем с комментированием.24 : 12=Д. Ищем частное способом подбора. Пробуем в частном 2 и проверяем.12 x 2=24, 24=24, значит, 24 : 12=2

Раз — подняться, потянуться,Два — нагнуть, разогнуться,Три — в ладоши, три хлопка,Головою три кивка.На четыре — руки шире,Пять — руками помахать,Шесть — на место ти.

VI. Закрепление пройденного материала.

1. №2 – Самостоятельно, с последующей проверкой. Дети для проверки обмениваются тетрадями. Тот, кто решил первым, записывает ответы на доске. Неправильно решенные примеры объясняются.

I столбик II столбик48 : 24 = 2 75 : 25 = 332 : 16 = 2 64 : 32 = 288 : 11 = 8 85 : 17 = 5

Совет 2: Как разделять числа

Тема деления чисел является одной из самых ответственных в математической программе 5 класса. Без овладения этими умениями немыслимо последующее постижение математики. Разделять числа доводиться в жизни всякий день. И неизменно полагаться на калькулятор не стоит. Дабы поделить два числа, надобно запомнить определенную последовательность действий.

Вам понадобится

• Лист бумаги в клетку,
• ручка либо карандаш

Инструкция

1. Запишите делимое и делитель на одной строке. Поделите их вертикальной чертой высотой в две строки. Проведите горизонтальную черту под делителем и делимым перпендикулярно предыдущей черте. Справа под этой чертой будет записываться частное. Ниже и левее делимого, под горизонтальной чертой, запишите нуль.

2. Перенесите одну самую левую, но еще не переносившуюся цифру делимого вниз под последнюю горизонтальную черту. Пометьте перенесенную цифру делимого точкой.

3. Сравните число под последней горизонтальной чертой с делителем. Если число поменьше делителя, то продолжите с шага 4, напротив перейдите к шагу 5.

4. Посмотрите, есть ли в делимом еще не переносившиеся цифры. Не переносившиеся цифры не помечены точками. Если такие цифры есть, то перейдите к шагу 2, напротив к шагу 7.

5. Рассчитайте следующую цифру частного. Посчитайте, какое наибольше число раз дозволено вычесть делитель из числа под последней горизонтальной чертой. Добавьте эту цифру к частному.

6. Вычислите дальнейший остаток. Помножьте делитель на последнюю цифру частного. Итог запишите со знаком минус под числом, находящимся под последней горизонтальной чертой. Под записанным числом проведите следующую горизонтальную черту. Вычтите последнее записанное число из предпоследнего. Итог запишите под только что проведенной чертой. Перейдите к шагу 4.

7. Деление чисел завершено. Под делителем сейчас записано частное 2-х чисел. Число под последней горизонтальной чертой на стороне делимого является остатком от деления.

Видео по теме

Обратите внимание! Изредка делитель представляет собой десятичную дробь. В этом случае, дабы поделить числа необходимо делитель заблаговременно привести к типичному виду

Для этого в делимом и делителе переносится запятая вправо на тоже число цифр, сколько есть в делителе позже запятой. После этого числа дозволено разделять, как традиционно.

• Как научить ребёнка правильно чистить зубы? (Развивалка для детей) — YouTube — как научить ребенка чистить зубы
• Как научить ребенка сидеть самостоятельно в 6-7 месяцев — как научить ребенка в 6 месяцев сидеть
• Как научить ребенка делать уроки самостоятельно? — как научить ребенка делать самостоятельно уроки
• Как научить ребенка грамотно писать без ошибок — как научить ребенка писать правильно без ошибок
• Как научить ребенка кататься на велосипеде двухколесном — как научить ребенка кататься на велосипеде двухколесном в 6 лет
• Как научить ребенка держать голову? — как научить ребенка держать голову
• Как научить читать ребенка 6 лет? — как научить ребенка 6 лет читать
• Как научить ребенка читать в домашних условиях — как правильно научить ребенка читать в домашних условиях
• Как научить ребенка читать в 4 года | Раннее развитие ребенка — как научить ребенка 4 лет читать
• Как научить сморкаться ребенка в 2-3 года: видео (Комаровский) — как научить ребенка сморкаться в 2 года

← Задача №6 — отметь в тетради точки как показано на чертеже соедини их отрезкамиАзартные игры →

Деление в столбик – правила

Для того, чтобы уметь делить в столбик необходимо знать некоторые правила. Именно об этом и пойдет далее речь. Ведь деление в столбик невозможно освоить если не знать элементарного – таблицы умножения. Считать простые примеры на умножение необходимо быстро и в уме. Это только в начале обычно дети пользуются черновиками, чтобы подобрать множитель, таким образом найти частное. Еще надобно уметь разбивать числа на сотни, десятки, тысячи – не путаться и в этих понятиях. Для наглядности, где делимое, где делитель, где частное можете изучить термины на изображении ниже.

Что нужно знать для деления в столбик?

Прежде, чем приступать к делению, следует проверить ребенка на знания элементарных правил. Ведь пропускать математику нельзя. А если пропуски все же были, то нужно изучить тот материал, что изучали ранее на уроках в школе

Понадобится обратить внимание на такие знания, как:

Запомнил ли школьник, как называются все элементы, участвующие в процессе деления.

Обратите внимание на знание таблицы умножения ребенком.
Еще ребенок должен усвоить, какие бывают разряды числа (единицы, десятки, сотни).

Пример: 

1. 57: 3, где 57 – это делимое, число, что разделяют на доли, а 3 – это делитель, указывающий, на сколько делить предыдущее число.
2. Определяемся, вначале какие единицы выделить в делимом для осуществления деления в столбик числа 57. Число 5 > 3.
3. Узнайте, сколько раз следует взять число 3, чтобы получить 5. Результат 3 · 1 = 3 ≤ 5. Значит подходит и 1 поставьте в качестве первой цифры частного.
4. Теперь вычитание: 5 — 3 = 2. Остаток 2 и единицу сносим, выходит 27.
5. Находим теперь, на какое число нужно умножить 3, чтобы результат был 27. Согласно таблице умножения 3 · 9 = 27.
6. Итого результат 19.

Умножение, деление – взаимосвязаны между собой, хотя и противоположные операции. Чтобы проверить, верно ли нашли частное, необходимо выполнить умножение. Потому таблица умножения и умение умножать на черновике без калькулятора всегда пригодится ребенку, также еще при умножении следует уметь правильно прибавлять, а при делении в столбик вычитать. В математики все действия с числами между собой взаимосвязаны.

Ниже смотрите пример деления в столбик 536 на 4. Действия с трехзначным делимым выполняются аналогично, что и с двухзначным.

Деление

Деление в школе начинают учить уже с третьего класса. Школьники только изучают азы процесса, выполняют самые простые примеры на это действие.

Примеры подобны умножению, только детей учат таблице деления, а не умножения. Школьники должны уловить саму суть, что означает поделить число на несколько частей, изучают, что такое делимое, делитель, частное. Узнают, как проверить умножением правильность решения примера или же задачи. В столбик дети еще не считают, так как даются самые простые примеры и все числа из таблицы умножения. Пример: 81 : 9 = 9.

Процесс деления в четвертом классе значительно усложняется. Детям дают вначале года вспомнить, что они учили в третьем классе, а далее уже начинают осваивать технику деления чисел в столбик. Именно за этот учебный год осваивают такие знания. Ниже приведен алгоритм решения примеров в столбик с подробным описанием процесса.

Здесь даже учтено то, что возможно будет остаток при делении, что число получится не цельным, а через запятую.

Деление на двузначное число с остатком

При делении на двузначное число с остатком рассуждать нужно так же.

1. Найдем частное.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 299 не на 34, а на 30.

9 – это пробная цифра частного, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 34 на 9.

306 больше, чем делимое 299. Значит, цифра 9 не подходит. Проверим цифру 8.

Значит, цифра 8 подойдет. Остаток меньше, чем делитель. Записываем в частном цифру 8.

Значение частного чисел 299 и 34 – 8 и остаток 27.

2. Рассмотрим еще один случай деления.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 191 не на 46, а на 40.

4 – это только пробная цифра, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 46 на 4.

Остаток 7 меньше, чем делитель 46. Значит, цифра частого 4 подходит, запишем ее.

Значение частного чисел 191 и 46 – 4 и остаток 7.

Деление в столбик – примеры для тренировки

Без множества примеров трудно освоить технику деления в столбик. Можно перерешать кучу примеров и тогда в любом случае материал усвоится хорошо. Ниже представлен пример деления числа 748 на 2. Давайте разберем этот простой пример деления в столбик.

1. У делимого следует выделить сотни, точнее их 7 у делимого. Для этой цифры подбираем множитель: 2 · 3 = 6 ≤ 7, значит подходит.
2. Пишем 6 под семеркой, а 3 под чертой, это одна из цифр частного.
3. Вычтем из 7 — 6 = 1, и сносим 4. Теперь подбираем множитель: 2 · 7 = 14 = 14 — результат верен. Вторая цифра частного 7.
4. Пишем 14 под 14, и сносим следующую цифру делимого 8. Подбираем множитель: 2 · 4 = 8 = 8, разница 0, число делится без остатка.
5. Итак, результат 374.

Пример деления

Этот пример решен, существует и множество других примеров, которые будут представлены далее по тексту на фото. Эти примеры – готовое решение домашних задач, где подробно расписан процесс деления в столбик, как находится каждая цифра частного. Когда все их перерешаете самостоятельно, то дело доведется до автоматизма и вы сможете решить задание любой сложности, пользуясь своим умением.

Делить в столбик, пожалуй, одна из самых непростых тем в математики. Как уже упоминалось, в процессе используют все четыре действия, (начиная от сложения, заканчивая умножением). Без знаний этих процессов никак не обойтись. Некоторые думают, что зачем знать, как делить, если есть калькуляторы. Но не всегда бывают они под рукой, а посчитать надо сдачи или другую величину, и знания пригодятся на практике. Далее изучите примеры на эту тему.

Пример деленияалгоритмы деления в столбикДеление трехзначного и четырехзначного числаДеление 693 на 3Деление чисел с нулямиДеление без остатка

Еще здесь на портале вы можете узнать много интересного на тему образования вот в этих текстах:

1. Сказка «Репка» по ролям в школе;
2. Сочинение по басне Крылова «Ворона и лисица»;
3. Сочинение на тему «Моя будущая профессия»;
4. Считалки для детей разного возраста;
5. Как правильно писать – на здоровье?

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

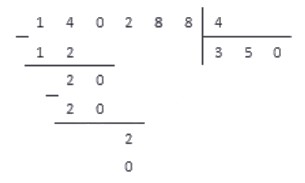
3. Выполняем операцию вычитания  и под чертой записываем результат.

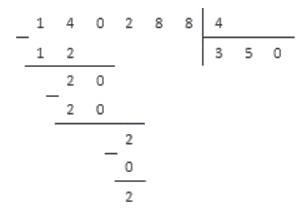
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

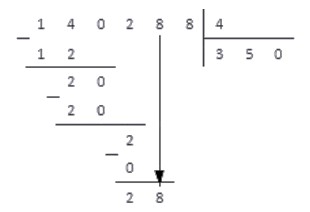
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

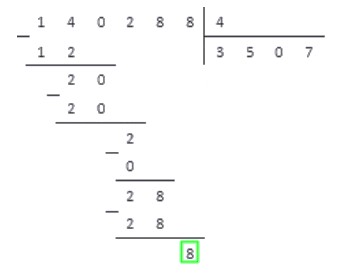
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

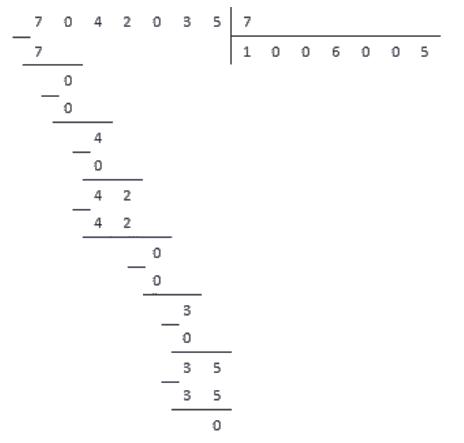
Ответ: 1006005

Урок математики в 3-м классе по теме «Деление двузначного числа на однозначное»

Цели:

Научить делить двузначное число на однозначное (внетабличные способы)
Развивать навыки устных вычислений, логическое мышление, внимание, речь учащихся.
Воспитывать культуру общения.

Ход урока

1. Приветствие

Долгожданный дан звонок

2. Актуализация опорных знаний.. Ситуация успеха.

Решите примеры и соберите слово.

— Что такое успех? (хорошие результаты в работе)

— Что нужно для достижения успеха?

— Я желаю вам всем успеха. А вы мысленно пожелайте успеха мне.

Индивидуальная работа у доски.

3.Ситуация затруднения. Устный счёт (с обратной связью)

— Найдите разность чисел в треугольниках, разделите полученный результат на число, записанное в квадрате, результат умножьте на число в круге, прибавьте число в четырёхугольнике, разделите на число в четырёхугольнике.

— Покажите результат. (20)

— Произведение чисел в кругах разделите на разность чисел в треугольниках, результат увеличьте на число, записанное в квадрате.

— Покажите результат. (53)

— Из суммы чисел в прямоугольниках вычтите произведение чисел в кругах, результат разделите на число в пятиугольнике. (У детей возникает затруднение 72 : 6)

— В чём проблема? (не умеем решать такие примеры)

— Вот сегодня на уроке мы должны этому научиться.

В верхнем левом углу доски появляется запись

4. Тема урока

Назовите тему урока.

Деление двузначного числа на однозначное.

— Как вы думаете, какие знания нам для этого понадобятся? (табличное деление, деление суммы на число, алгоритм)

— Хорошо, давайте вспомним всё, что мы уже знаем.

а) Деление за 1 минуту

(На доску вывешиваю таблицу с примерами на табличное деление. Дети на листочках записывают только ответы в течении 1 минуты. Подаю команду “Стоп!” и все сдают листочки. Сразу же выявляю победителя по количеству решённых примеров, а к концу урока проверяю правильность решения и утверждаю победителя или выявляю нового)

б) Проверка индивидуального задания у доски.

(вопрос к ученику, работавшему у доски)

— Объясни, какими способами ты пользовался?

— Какой из этих способов нам сегодня пригодится?

5. Работа над решением проблемы.

а) Работа в тетради. Каллиграфическая минутка.

— Пропишите число 63.

— На какие однозначные числа делится число 63? (7 и 9)

— Так какая у нас сегодня задача на уроке? (Научиться делить двузначное число на однозначное)

б) Представьте число 63 в виде суммы двух слагаемых, каждое из которых делится на 3.

63 : 3 = (60 + 3) : 3 = 60 : 3 + 3 : 3 =

— Каким способом деления суммы на число воспользовались?

(Каждое слагаемое разделили на число и результаты сложили)

Вывод: Для того, чтобы разделить число 63 что нам пришлось с ним сделать?

(Заменить суммой разрядных слагаемых)

— А затем? (разделить каждое слагаемое на 3)

— Потом? (результаты сложить)

— Вернёмся к нашей проблеме.

— Какая проблема возникла в устном счёте?

— Давайте решим по такому же плану.

— Представьте число 72 в виде суммы двух слагаемых, каждое из которых делится на 6.

72 : 6 = (60 + 12) : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12

Вывод: В первом случае заменили суммой разрядных слагаемых, а во втором – суммой удобных слагаемых.

в) — Давайте составим план наших действий

— Что мы делали сначала?

— Сравните с алгоритмом умножения двузначного числа на однозначное

6. Физминутка

7. Первичное закрепление новых знаний.

Используя составленный алгоритм найдём значения нескольких выражений.

(работа у доски с подробным объяснением и развёрнутой записью)

7. Работа с учебником

С.13 №2 1 столбик с места с комментированием

— Какая проблема возникла у нас на уроке?

— Удалось нам её решить?

8. Первичный контроль и оценка.

1) Запишите выражение и найдите его значение

2) Составьте задачу по этому выражению.(дети составляют задачи разных видов и решают их устно)

3) Дополните условие задачи так, чтобы она стала составной.

Решите задачу в тетради.

9. Итог урока.

— Какую проблему решали на уроке?

— Научились выполнять внетабличное деление двузначного числа на однозначное?

— Хотите себя проверить?

Рефлексия (Каждому ученику выдаётся карточка, на которой примеры трёх уровней сложности.

Ученик имеет право выбрать любой из этих уровней.)

1уровень	2 уровень	3 уровень
1. 86 : 2 =	1. 39 : 3 =	1. 78 : 3 =
2. 93 : 3 =	2. 69 : 3 =	2. 90 : 5 =
3. 68 : 2 =	3. 48 : 2 =	3. 75 : 3 =
4. 96 : 3 =	4. 75 : 5 =	4. 42 : 3 =
5. 88 : 4 =	5. 60 : 4 =	5. 96 : 6 =

Вывешиваю правильные ответы. Дети проверяют и оценивают свою работу.

— Каждый правильный ответ 1 балл

— Покажите (карточкой) сколько баллов заработали.